K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
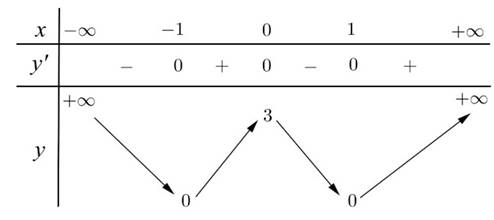
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)
TN
1 giờ trước (15:44)
Mình nhìn rõ biểu thức trong ảnh là:
$$
V = \sqrt[3]{\,(x^2 - 4)^2\,}.
$$
---
### Phân tích:
* Đây là căn bậc 3 của $(x^2 - 4)^2$.
* Vì căn bậc 3 **luôn xác định với mọi số thực**, nên biểu thức có **tập xác định** là $\mathbb{R}$ (tất cả số thực).
---
### Biến đổi đơn giản hơn:
$$
V = \sqrt[3]{(x^2 - 4)^2} = \big|x^2 - 4\big|^{\tfrac{2}{3}}.
$$
---
✅ Kết luận:
* Tập xác định: $D = \mathbb{R}$.
* Dạng đơn giản: $V = |x^2 - 4|^{2/3}$.
8 tháng 9
c: \(y=-x^2+2x+3\)
=>\(y^{\prime}=-2x+2\)
Đặt y'<0
=>-2x+2<0
=>-2x<-2
=>x>1
=>Hàm số nghịch biến trên (1;+∞)
Đặt y'>0
=>-2x+2>0
=>-2x>-2
=>x<1
=>Hàm số đồng biến trên (-∞;1)
d: \(y=\frac13x^3+3x^2+5x+2\)
=>\(y^{\prime}=\frac13\cdot3x^2+3\cdot2x+5=x^2+6x+5=\left(x+1\right)\left(x+5\right)\)
Đặt y'>0
=>(x+1)(x+5)>0
=>\(\left[\begin{array}{l}x>-1\\ x<-5\end{array}\right.\)
=>Hàm số đồng biến trên các khoảng (-1;+∞) và (-∞;-5)
Đặt y'<0
=>(x+1)(x+5)<0
=>-5<x<-1
=>Hàm số nghịch biến trên khoảng (-5;-1)
PD
0
22 tháng 11 2016
Đặt MA=x \(\Rightarrow\)MB= 24-x với \(x\in\left[0;24\right]\)
Đặt f(x)=MC+MD=\(\sqrt{MA^2+AC^2}+\sqrt{MB^2+BD^2}=\sqrt{x^2+10^2}+\sqrt{\left(24-x^2\right)+30^2}\)
Ta xét hàm f(x) trên đoạn [0;24]
\(f'\left(x\right)=\frac{x}{\sqrt{x^2+10^2}}-\frac{24-x}{\sqrt{\left(24-x\right)^2+30^2}}\\ =\frac{MA}{MC}-\frac{MB}{MD}\)
\(f'\left(x\right)=0\Leftrightarrow\frac{MA}{MC}-\frac{MB}{MD}=0\Leftrightarrow\frac{MA}{MC}=\frac{MB}{MD}\)
từ đó suy ra hai tam giác vuông \(\Delta MAC\) và \(\Delta MBD\) đồng dạng
\(\Rightarrow\frac{MA}{MC}=\frac{MB}{MD}=\frac{AC}{BD}=\frac{1}{3}\)
Vậy \(MA=\frac{24}{3+1}=6\)(m) và MB=24-6=18(m)
a) Gọi K' là giao điểm của BI và EF, S là giao điểm của EJ và AB.
Ta có \(\left(FSBA\right)=-1\) (hàng điều hòa quen thuộc). Mặt khác, dễ thấy K'B là trung trực của FJ nên K'B cũng là tia phân giác của \(\widehat{FK'S}\)
Do đó, \(\widehat{AK'B}=90^o\). Khi đó tam giác AK'B vuông tại K' có trung tuyến K'M nên \(K'M=MB=\dfrac{1}{2}AB\)
Từ đó suy ra tam giác MK'B cân tại M \(\Rightarrow\widehat{MK'B}=\widehat{MBK'}=\widehat{K'BC}\)
Do đó MK'//BC. Chú ý rằng MN là đường trung bình của tam giác ABC \(\Rightarrow\) MN//BC. Vậy \(K'\in MN\) hay K' chính là giao điểm của MN và JE. Điều này có nghĩa là \(K'\equiv K\).
Như vậy, \(K,B,I\) thẳng hàng và \(\widehat{AKB}=90^o\) hay \(AK\perp BI\)
Lại có \(FJ\perp BI\) nên AK//FJ hay AK//HJ.
Tương tự, ta cũng có AH//KJ nên tứ giác AKJH là hình bình hành.
\(\Rightarrow\) HK, AJ cắt nhau tại trung điểm mỗi đoạn, hay JA đi qua trung điểm của HK.
câu a ý 2:
Gọi U là giao điểm của EF và BC, P là trung điểm BC, X là điểm chính giữa cung BC không chứa D của (O).
Có \(\widehat{XIB}=\widehat{IAB}+\widehat{IBA}=\widehat{XCB}+\widehat{IBC}=\widehat{XBC}+\widehat{IBC}=\widehat{XBI}\) nên tam giác XBI cân tại X \(\Rightarrow XB=XI\)
Tương tự, ta cũng có \(XB=XC=XI\) nên X là tâm (IBC)
Dễ thấy \(\widehat{XBD}=\widehat{XCD}=90^o\) nên XB, XC là tiếp tuyến tại B và C của (X).
\(\Rightarrow DC^2=DP.DX=DT.DG\) \(\Rightarrow\) Tứ giác TPXG nội tiếp.
\(\Rightarrow\widehat{DPT}=\widehat{XGT}=\widehat{XTG}=\widehat{XPG}\)
\(\Rightarrow90^o-\widehat{DPT}=90^o-\widehat{XPG}\)
\(\Rightarrow\widehat{UPT}=\widehat{UPG}\) . Do \(\widehat{UPG}+\widehat{GPC}=180^o\)
\(\Rightarrow\) \(\widehat{GPC}+\widehat{UPT}=180^o\)
Vì D là giao điểm của 2 tiếp tuyến tại B và C của đường tròn (X) nên GD là đối trung của tam giác GBC
\(\Rightarrow\widehat{BGT}=\widehat{PGC}\)
Lại có \(\widehat{GTB}=\widehat{GCP}\) \(\Rightarrow\Delta GTB\sim\Delta GCP\) \(\Rightarrow\widehat{GBT}=\widehat{GPC}\)
Lại có \(\widehat{GBT}=\widehat{GIT}\) nên \(\widehat{GPC}=\widehat{GIT}\)
Kết hợp với \(\widehat{GPC}+\widehat{UPT}=180^o\), ta có \(\widehat{GIT}+\widehat{UPT}=180^o\)
\(\Rightarrow\) Tứ giác ITPJ nội tiếp.
Mặt khác, \(\left(BCJU\right)=-1\) và P là trung điểm BC nên \(\overline{UJ}.\overline{UP}=\overline{UB}.\overline{UC}\) (hệ thức Maclaurin)
\(\Rightarrow P_{U/\left(ITPJ\right)}=P_{U/\left(X\right)}\)
\(\Rightarrow\) U nằm trên trục đẳng phương của đường tròn (ITPJ) và (X), mà IT là trục đẳng phương của 2 đường tròn này nên U, I, T thẳng hàng.
Xét cực và đối cực đối với (I). Kí hiệu \(d_Y\) là đối cực của Y đối với (I).
Ta có \(\left(BCJU\right)=-1\) \(\Rightarrow J\in d_U\)
Lại có \(U\in EF\equiv d_A\Rightarrow A\in d_U\)
Do đó \(JA\equiv d_U\) \(\Rightarrow JA\perp UI\) hay \(JA\perp IT\) (đpcm)