Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

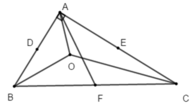
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D

1.
a) Xét ΔADE có :
HE là đường trung tuyến của AD HA=HD )(1)
Ta thấy HC=12BC ( AH là đường trung tuyến của BC )
Mà BC = CE (gt )
⇒HC=12CE (2)
Từ (1) và (2) ⇒C là trọng tâm của ΔADE
b) Hơi khó đấy :)
Xét ΔAHB và ΔAHC có :
HAHA chung
HB=HC ( AH là đường trung tuyến của BC )
AB=AC( ΔABC cân tại A )
Do đó : ΔAHB=ΔAHC(c−c−c)
⇒AHBˆ=AHCˆ( hai góc tương ứng )
Mà AHBˆ+AHCˆ=1800
⇒AHB^=AHC^=1800/2=90o
Xét ΔAHEvà ΔHED có :
HEHE chung
HA=HD( HE là đường trung tuyến của AD )
AHEˆ=DHEˆ(=900)
Do đó : ΔAHE=ΔDHE ( hai cạnh góc vuông )
⇒AEHˆ=DEHˆ ( góc tương ứng ) (*)
Vì C là trọng tâm của ΔAED là đường trung tuyến của DE )
Xét vuông tại H có : HM là đường trung tuyến nối từ đỉnh H đến DE
⇒HM=DM (1)
Lưu ý : Trong tam giác vuông , đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền . Tức HM=12DE Mà 12DE=DM⇒HM=DM
Trở lại vào bài :
Mặt khác DM=ME(cmt)(2)
Từ (1) và (2) ⇒HM=ME
⇒ΔHME⇒ΔHME cân tại M
⇒MHEˆ=MEHˆ
Dễ thấy MEHˆ=HEAˆ(cmt)
⇒MHEˆ=HEAˆ
mà hai góc này ở vị trí so le trong
⇒HM⇒HM//AE(đpcm)
2.
a) ta có: \(\Delta OAB,\Delta OAC\) có diện tích bằng nhau và cùng đáy OA nên khoảng cách từ B , C kẻ đến OA
nên BH=CK
b) gọi AK giao với BC tại M
Xét \(\Delta BHM\)và \(\Delta CKM\) có:
..........
3.
a. xét tgiac ADC và tgiac ADB có
AD là cạnh chung
góc DAB = góc DAC(gt)
AB=AC(gt)
vậy tg ADC=tg ADB(c.g.c)
b.theo cminh cau a ta có DB=DC(2 cạnh tương ứng)
nên AD là đường trung tuyến ứng với cạnh BC mà G là trọng tâm tâm giác ABC nên A D G thẳng hàng
k mk nha thack ae
Bài 1 :
a) Vì AH = HD => EH là đg trung tuyến của tg ADE
Khi đó C thuộc đg trung tuyến EH (1)
Do tam giác ABC cân tại A
mà AH là đường cao của tam giác ABC
=> AH là đg trung trực của tam giác ABC
=> BH = CH
=> BH = CH = \(\frac{1}{2}\)BC
Lại do BC = CE
=> CH = \(\frac{1}{2}\) CE
hay CE = \(\frac{2}{3}\) EH (2)
Từ (1); (2) => C là trọng tâm của tam giác ADE.
b) Có : AH là đường cao của ΔABC
⇒ Góc AHC = 90
⇒ Góc DHC = 90 (kề bù)
Xét ΔAHE và ΔDHE có:
+ AH = DH (gt)
+ Góc AHE = góc DHE = 90
+ HE chung
⇒ ΔAHE = ΔDHE
⇒ Góc EAH = góc EDH (1)
Lại có: Tia AC cắt DE tại M
Mà C là trong tâm của ΔADE
⇒ AM là trung tuyến của ΔADE
⇒ M là trung điểm của DE
Mà ΔDHE là tam giác vuông tại H (do DHE = 90 )
⇒ HM là đường trung tuyến của cạnh huyền
⇒ HM = DM = EM
⇒ ΔHMD cân tại M
⇒ Góc MHD = góc MDH (2)
Từ (1) + (2) ⇒ Góc EAH = góc MHD
Mà hai góc này là hai góc đồng vị
⇒ AE // HM (đpcm)

A là trực tâm của tam giác ABC vì A là giao của 2 đường cao AB và AC
Chọn C
Xét ΔABC có
AC là đường cao ứng với cạnh AB
AB là đường cao ứng với cạnh AC
AC cắt AB tại A
Do đó: A là trực tâm của ΔABC