NP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 9 2016
Chỗ khoanh bút bi thì là biến đổi tương đương từ biểu thức trước nó thôi bạn.
Còn chỗ khoanh mờ, là công thức nghiệm của hàm \(\cos x =0\)
CM
4 tháng 12 2019
I, J lần lượt là trung điểm của AC và BC nên IJ // AB. Do đó giao tuyến của (IJK) với (ABD) là đường thẳng đi qua K và song song với AB cắt AD tại H. Vậy IJ // KH // AB. Ta có ∆BJK = ∆AIH ⇒ JK = IH. Hơn nữa KH ≠ IJ.
Vậy thiết diện là hình thang cân IJKH
Đáp án A
NV
5
21 tháng 2 2020
số số hạng là :
\(\left(2018-1\right):1+1=2018\)
tổng trên bằng
\(\left(\frac{1}{2018}+\frac{1}{2}\right).2018:2\)
\(=\frac{1010}{2018}.2018:2\)
\(=1010:2=505\)
P/s : ko chắc >: hình như sai
21 tháng 2 2020
Công thức tính tổng
{(Số đầu + số cuối). số số hạng } :2
8 tháng 7 2021
Ví dụ 3:
a, - Chọn ngẫu nhiên 3 học sinh từ 35 học sinh và sắp xếp vào 3 vị trí có: \(A^3_{35}=39270\) (cách)
b, - Chọn 1 học sinh làm lớp trưởng từ 15 học sinh nam có 15 cách.
- Chọn 2 học sinh từ 34 học sinh còn lại và sắp xếp vào 2 vị trí có \(A^2_{34}\) cách.
⇒ Có: \(15.A^2_{34}=16830\) (cách)
c, - Chọn 2 học sinh từ 20 học sinh nữ và sắp xếp vào 2 vị trí lớp trưởng, lớp phó có \(A^2_{20}\) cách.
- Chọn 1 học sinh từ 33 học sinh còn lại có 33 cách.
⇒ Có: \(A^2_{20}.33=12540\) (cách)
d, - Chọn 3 học sinh từ 15 học sinh nam xếp vào 3 vị trí có \(A^3_{15}\) cách.
⇒ Có: \(A^3_{15}\) cách chọn 3 vị trí mà không có bạn nữ nào.
⇒ Có: \(39270-A^3_{15}=36540\) cách chọn 3 vị trí để có ít nhất một bạn nữ.
HP
12 tháng 9 2021
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
TG
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
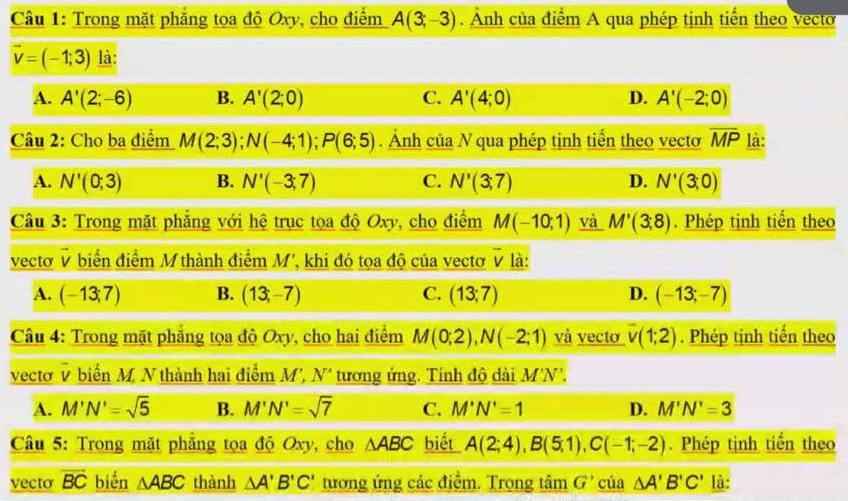
1.
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)
16 tháng 8 2023
tham khảo:
a) AA’ vuông góc với mặt phẳng (P)
b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là giao điểm của a với (P).
TG
4
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
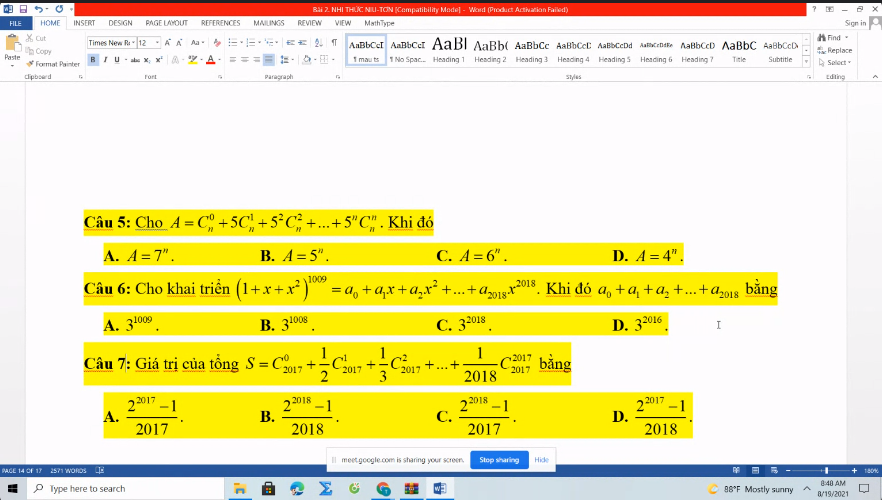
2.
Xét khai triển:
\(\left(1+x\right)^{2017}=C_{2017}^0+C_{2017}^1.x+C_{2017}^2x^2+...+C_{2017}^{2017}x^{2017}\)
Cho \(x=1\) ta được:
\(2^{2017}=C_{2017}^0+C_{2017}^1+...+C_{2017}^{2017}\)
\(\Rightarrow C_{2017}^1+C_{2017}^2+...+C_{2017}^{2017}=2^{2017}-C_{2017}^0=2^{2017}-1\)
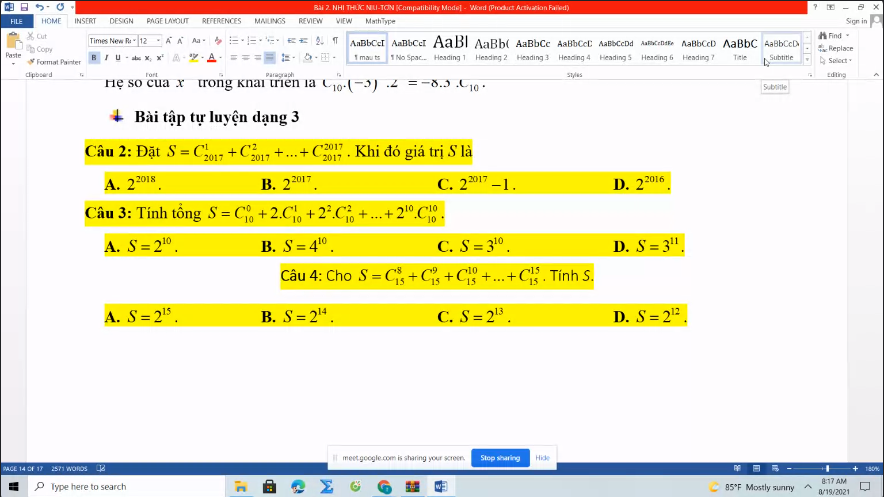
3.
Xét khai triển:
\(\left(1+x\right)^{10}=C_{10}^0+C_{10}^1x+...+C_{10}^{10}x^{10}\)
Thay \(x=2\) ta được:
\(3^{10}=C_{10}^0+2C_{10}^1+2^2C_{10}^2+...+2^{10}C_{10}^{10}\)
\(\Rightarrow S=3^{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 8 2021
4.
Xét khai triển:
\(\left(1+x\right)^{15}=C_{15}^0+C_{15}^1x+...+C_{15}^{15}x^{15}\)
Thay \(x=1\) ta được:
\(2^{15}=C_{15}^0+C_{15}^1+...+C_{15}^{15}\)
Mặt khác, áp dụng công thức: \(C_n^k=C_n^{n-k}\) ta có:
\(C_{15}^0=C_{15}^{15}\)
\(C_{15}^1=C_{15}^{14}\)
...
\(C_{15}^7=C_{15}^8\)
Cộng vế:
\(C_{15}^0+C_{15}^1+...+C_{15}^7=C_{15}^8+C_{15}^9+...+C_{15}^{15}\)
\(\Rightarrow C_{15}^0+C_{15}^1+...+C_{15}^{15}=2\left(C_{15}^8+C_{15}^9+...+C_{15}^{15}\right)\)
\(\Rightarrow2S=2^{15}\)
\(\Rightarrow S=2^{14}\)
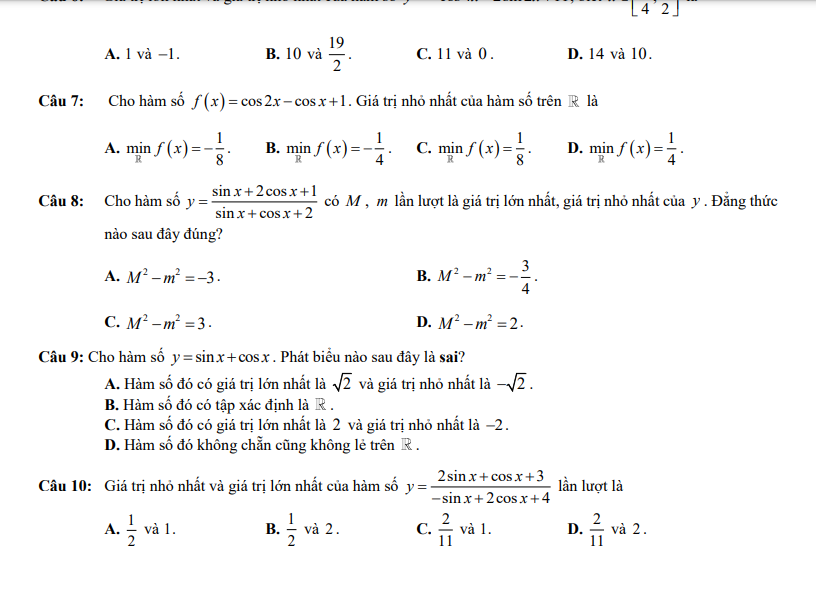
bấm vào tên người muốn kb rồi kb thui
Bn chọn một người muốn kb, xong vào trang cá nhân ở đó. Có chữ "kết bạn" thì bn ấn vào và cuối cùng là chờ người ấy đồng ý thui. Dễ mà bn. K nha!