Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

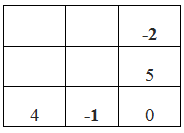
Cách làm như sau: gọi 3 số còn lại trong 4 ô đầu tiên lần lượt là a, b, c như hình dưới:

Tích 3 ô đầu tiên là: a.b.6
Tích 3 ô thứ hai là: b.6.c
Theo bài, tích 3 số ở ba ô liên tiếp đều bằng 120 nên:
a.b.6 = b.6.c => a = c
Từ đó ta tìm ra qui luật: các số ở cách nhau 2 ô đều bằng nhau. Ta điền 6 và -4 vào bảng, như sau:

Vậy số còn lại bằng (-5) vì: (-5).(-4).6 = 120.


Nhận xét:
Tháng bạn Minh nhận được nhiều điểm tốt nhất: Tháng 11(7 điểm)
Tháng bạn Minh nhận được ít điểm tốt nhất: Tháng 2(1 điểm)
Trung bình bạn Minh được khoảng: 4-5 điểm tốt/tháng.
Bạn Minh nhận được tất cả: 39 điểm tốt.

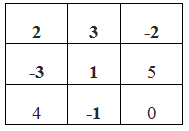
Vì điền mỗi số vào một ô nên ta có tổng 9 số ở 9 ô vuông là:
\(1+\left(-1\right)+2+\left(-2\right)+3+\left(-3\right)+4+5+0=9\)
Do đó tổng 3 số ở mỗi dòng, mỗi cột hoặc mỗi đường chéo sẽ là 3.
Từ đó:
- Với ô trống còn lại ở cột 3 điền là \(-2\) vì: \(3-5-0=-2\) (lấy tổng trừ đi hai ô còn lại).
- Với ô trống còn lại ở hàng 3 điền là \(-1\) vì: \(3-4-0=-1\)
Khi đó ta được bảng:
- Với ô trống ở giữa trên đường chéo ta điền là \(1\) bởi vì: \(3-4-\left(-2\right)=1\)
Làm tương tự với các ô trống còn lại ta sẽ được bảng kết quả như sau:

|
a |
-2 |
18 |
12 |
-2 |
-5 |
|
b |
3 |
-18 |
-12 |
6 |
-5 |
|
a + b |
1 |
0 |
0 |
4 |
-10 |
Giải:
a) Xác suất thực nghiệm để gieo được đỉnh số 2 là:
\(5:20=\dfrac{5}{20}\)\(=\dfrac{1}{4}\)
Vậy xác suất thực nghiệm để giao được đỉnh số 2 là \(\dfrac{1}{4}\).
b) Xác suất thực nghiệm để gieo được đỉnh có số chẵn là:
\(\left(5+5\right):20=\dfrac{10}{20}=\dfrac{1}{2}\)
Vậy xác suất thực nghiệm để gieo được đỉnh có số chẵn là \(\dfrac{1}{2}\).