K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
0
LA
9 tháng 1 2024
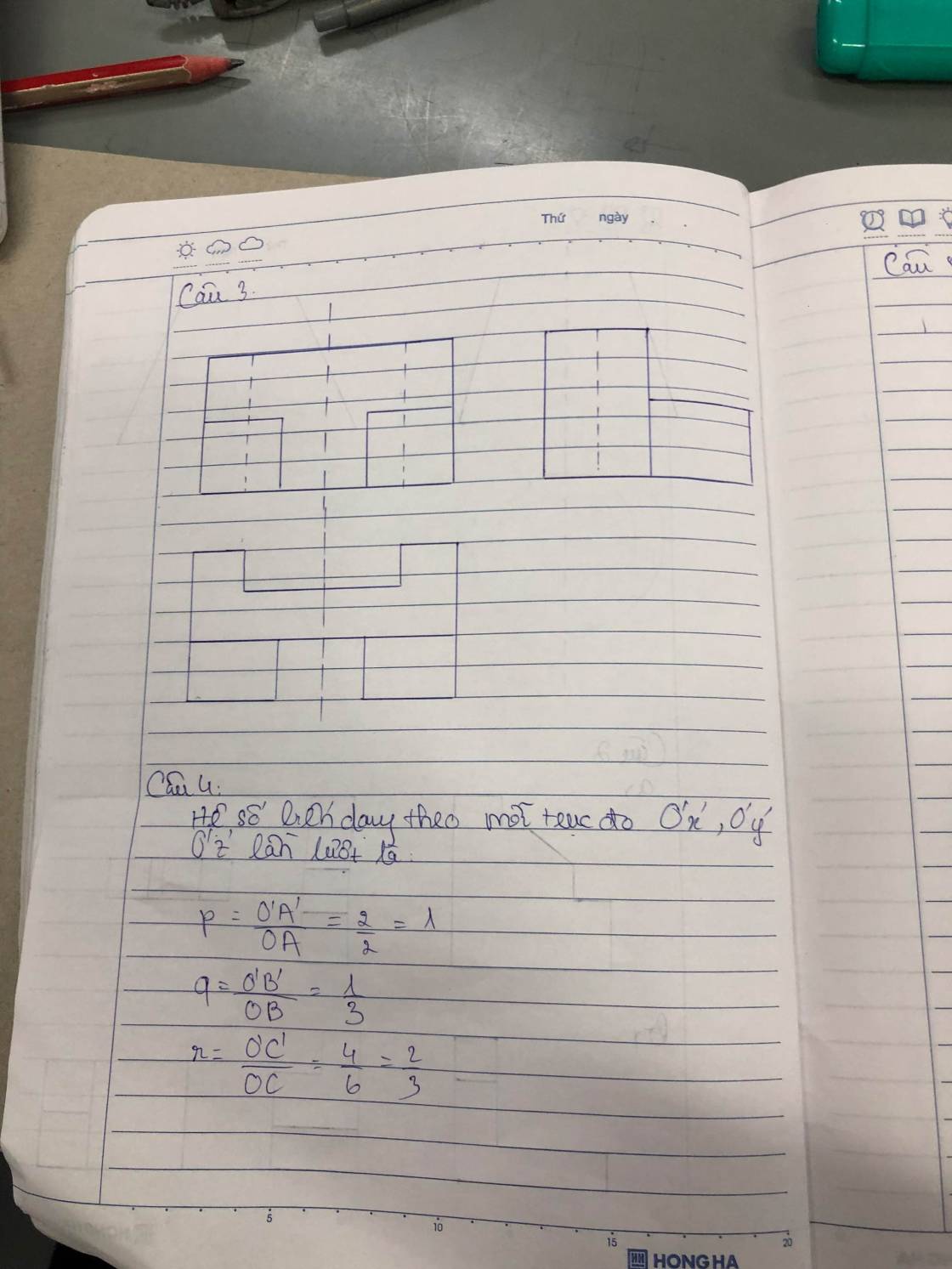
Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng lớn (dần tới \( + \infty \)).
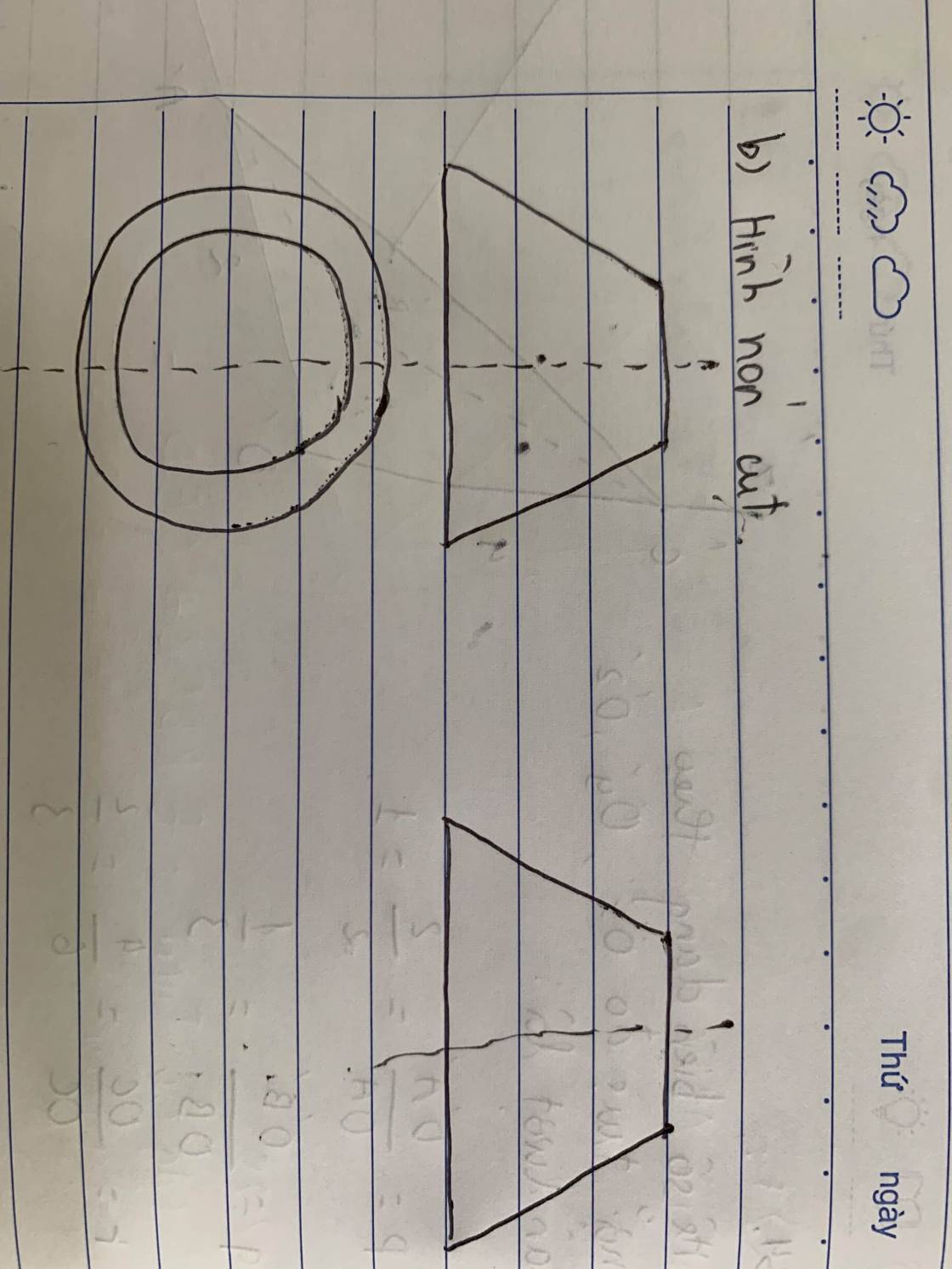
b)
Giá trị \(f\left( x \right)\) dần về 0 khi \(x\) càng bé (dần tới \( - \infty \)).
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
1.
\(u_{n+1}=4u_n+3.4^n\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{4}\left(n+1\right).4^{n+1}=4\left[u_n-\dfrac{3}{4}n.4^n\right]\)
Đặt \(u_n-\dfrac{3}{4}n.4^n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=2-\dfrac{3}{4}.4=-1\\v_{n+1}=4v_n\end{matrix}\right.\)
\(\Rightarrow v_n=-1.4^{n-1}\)
\(\Rightarrow u_n=\dfrac{3}{4}n.4^n-4^{n-1}=\left(3n-1\right)4^{n-1}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
2.
\(a_n=\dfrac{a_{n-1}}{2n.a_{n-1}+1}\Rightarrow\dfrac{1}{a_n}=2n+\dfrac{1}{a_{n-1}}\)
\(\Leftrightarrow\dfrac{1}{a_n}-n^2-n=\dfrac{1}{a_{n-1}}-\left(n-1\right)^2-\left(n-1\right)\)
Đặt \(\dfrac{1}{a_n}-n^2-n=b_n\Rightarrow\left\{{}\begin{matrix}b_1=2-1-1=0\\b_n=b_{n-1}=...=b_1=0\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{a_n}=n^2+n\Rightarrow a_n=\dfrac{1}{n^2+n}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 10 2019
ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)
TD
52
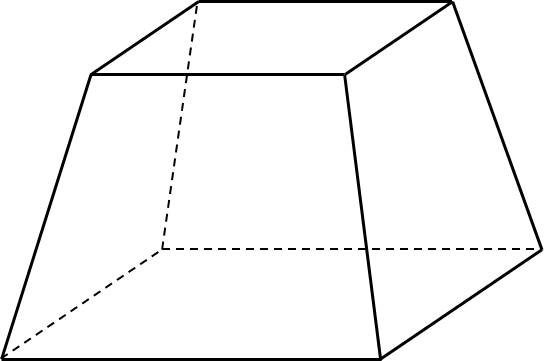
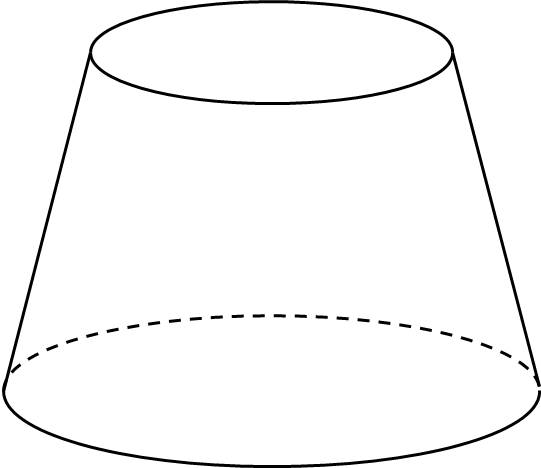
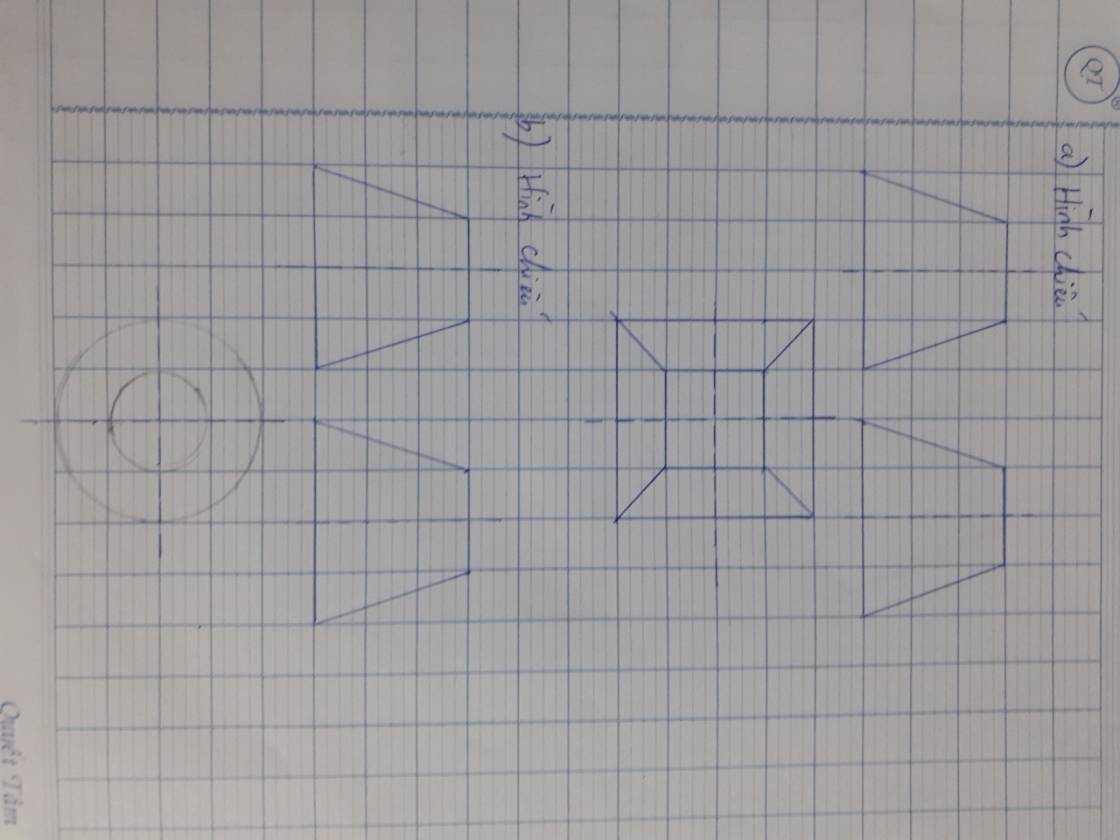
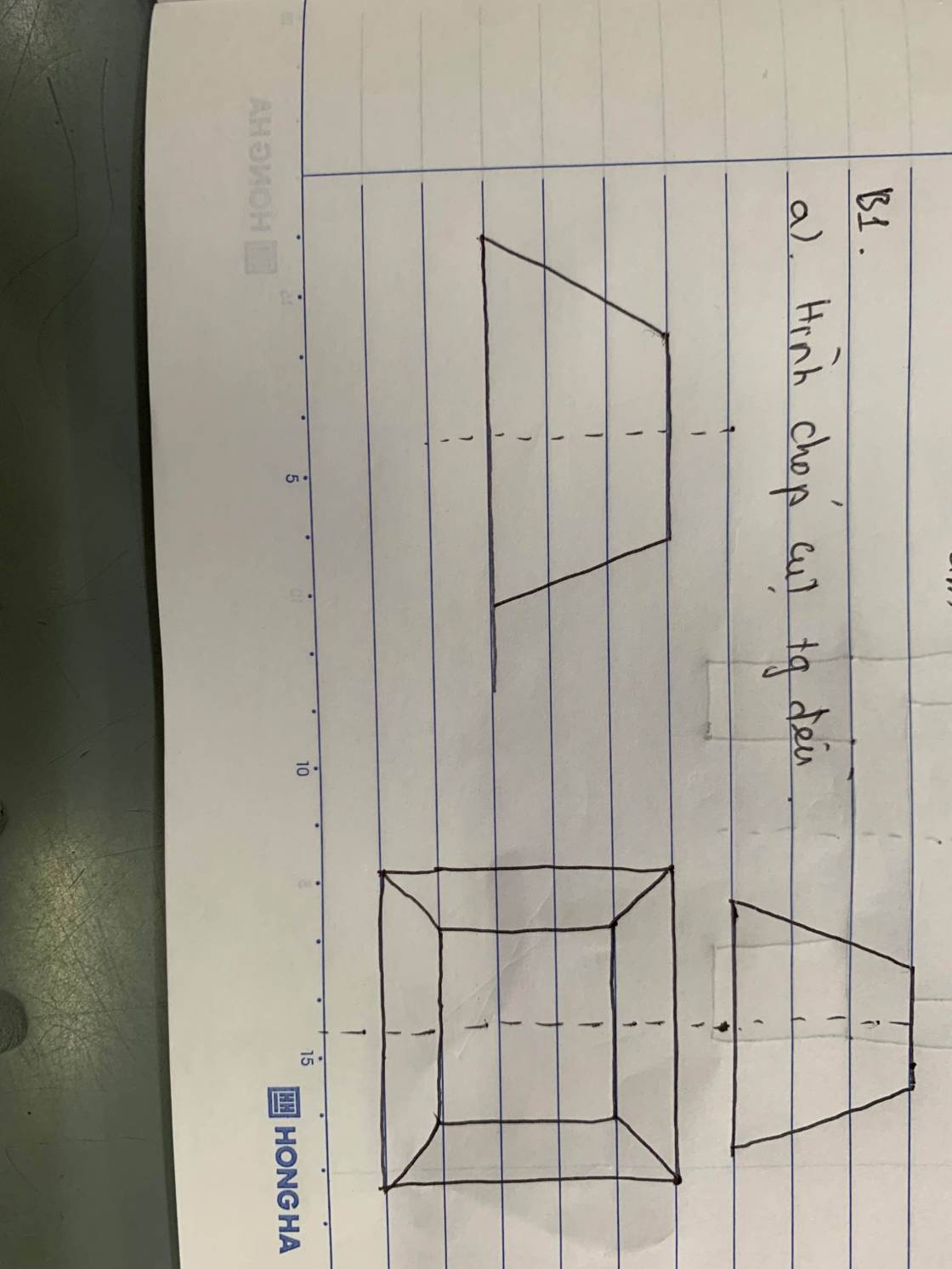
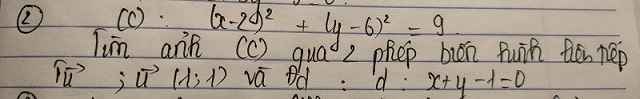
Đặt \(\left(\dfrac{x}{4};\dfrac{y}{2};z\right)=\left(a;b;c\right)\Rightarrow a;b;c\ge0\)
Từ giả thiết \(\Rightarrow16^a+16^b+16^c=34\)
Do \(a;b;c\ge0\Rightarrow\left\{{}\begin{matrix}16^a\ge1\\16^b\ge1\\16^c\ge1\\16^{a+b}\ge1\end{matrix}\right.\)
\(\Rightarrow\left(16^a-1\right)\left(16^b-1\right)+\left(16^{a+b}-1\right)\left(16^c-1\right)\ge0\)
\(\Leftrightarrow16^{a+b}-16^a-16^b+1+16^{a+b+c}-16^{a+b}-16^c+1\ge0\)
\(\Leftrightarrow16^{a+b+c}\ge16^a+16^b+16^c-2=32\)
\(\Leftrightarrow a+b+c\ge log_{16}32=\dfrac{5}{4}\)
\(P_{min}=\dfrac{5}{4}\) khi \(\left(a;b;c\right)=\left(0;0;\dfrac{5}{4}\right)\) và hoán vị
Đặt (𝑥4;𝑦2;𝑧)=(𝑎;𝑏;𝑐)⇒𝑎;𝑏;𝑐≥0(4x;2y;z)=(a;b;c)⇒a;b;c≥0
Từ giả thiết ⇒16𝑎+16𝑏+16𝑐=34⇒16a+16b+16c=34
Do 𝑎;𝑏;𝑐≥0⇒{16𝑎≥116𝑏≥116𝑐≥116𝑎+𝑏≥1a;b;c≥0⇒⎩⎨⎧16a≥116b≥116c≥116a+b≥1
⇒(16𝑎−1)(16𝑏−1)+(16𝑎+𝑏−1)(16𝑐−1)≥0⇒(16a−1)(16b−1)+(16a+b−1)(16c−1)≥0
⇔16𝑎+𝑏−16𝑎−16𝑏+1+16𝑎+𝑏+𝑐−16𝑎+𝑏−16𝑐+1≥0⇔16a+b−16a−16b+1+16a+b+c−16a+b−16c+1≥0
⇔16𝑎+𝑏+𝑐≥16𝑎+16𝑏+16𝑐−2=32⇔16a+b+c≥16a+16b+16c−2=32
⇔𝑎+𝑏+𝑐≥𝑙𝑜𝑔1632=54⇔a+b+c≥log1632=45
𝑃𝑚𝑖𝑛=54Pmin=45 khi (𝑎;𝑏;𝑐)=(0;0;54)(a;b;c)=(0;0;45) và hoán vị