Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(C=\left(\dfrac{12}{199}+\dfrac{23}{200}-\dfrac{34}{201}\right)\cdot\dfrac{3-2-1}{6}=0\)

1. \(A=\dfrac{2\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}{4\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}=\dfrac{2}{4}=\dfrac{1}{2}\)
2. \(B=\dfrac{1^2.2^2.3^2.4^2}{1.2^2.3^2.4^2.5}=\dfrac{1}{5}\)
3.\(C=\dfrac{2^2.3^2.\text{4^2.5^2}.5^2}{1.2^2.3^2.4^2.5.6^2}=\dfrac{125}{36}\)
4.D=\(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right).\dfrac{4}{9}.\dfrac{1}{16}=\dfrac{19}{30}.\dfrac{1}{36}=\dfrac{19}{1080}\)

Bài 1:
a, \(\left(x-2\right)^2=9\)
\(\Rightarrow x-2\in\left\{-3;3\right\}\Rightarrow x\in\left\{-1;5\right\}\)
b, \(\left(3x-1\right)^3=-8\)
\(\Rightarrow3x-1=-2\Rightarrow3x=-1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
c, \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)
\(\Rightarrow x+\dfrac{1}{2}\in\left\{-\dfrac{1}{4};\dfrac{1}{4}\right\}\)
\(\Rightarrow x\in\left\{-\dfrac{3}{4};-\dfrac{1}{4}\right\}\)
d, \(\left(\dfrac{2}{3}\right)^x=\dfrac{4}{9}\)
\(\Rightarrow\left(\dfrac{2}{3}\right)^x=\left(\dfrac{2}{3}\right)^2\)
Vì \(\dfrac{2}{3}\ne\pm1;\dfrac{2}{3}\ne0\) nên \(x=2\)
e, \(\left(\dfrac{1}{2}\right)^{x-1}=\dfrac{1}{16}\)
\(\Rightarrow\left(\dfrac{1}{2}\right)^{x-1}=\left(\dfrac{1}{2}\right)^4\)
Vì \(\dfrac{1}{2}\ne\pm1;\dfrac{1}{2}\ne0\) nên \(x-1=4\Rightarrow x=5\)
f, \(\left(\dfrac{1}{2}\right)^{2x-1}=8\) \(\Rightarrow\left(\dfrac{1}{2}\right)^{2x-1}=\left(\dfrac{1}{2}\right)^{-3}\) Vì \(\dfrac{1}{2}\ne\pm1;\dfrac{1}{2}\ne0\) nên \(2x-1=-3\) \(\Rightarrow2x=-2\Rightarrow x=-1\) Chúc bạn học tốt!!!
3. Gọi d là ƯCLN(2n + 3, 4n + 8), d ∈ N*
\(\Rightarrow\hept{\begin{cases}2n+3⋮d\\4n+8⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(2n+3\right)⋮d\\4n+8⋮d\end{cases}\Rightarrow}\hept{\begin{cases}4n+6⋮d\\4n+8⋮d\end{cases}}}\)
\(\Rightarrow\left(4n+8\right)-\left(4n+6\right)⋮d\)
\(\Rightarrow2⋮d\)
\(\Rightarrow d\in\left\{1;2\right\}\)
Mà 2n + 3 không chia hết cho 2
\(\Rightarrow d=1\)
\(\RightarrowƯCLN\left(2n+3,4n+8\right)=1\)
\(\Rightarrow\frac{2n+3}{4n+8}\) là phân số tối giản.

2155-(174+2155)+(-68+174)=2155-174-2155-68+174
= -68
( 1 - \(\dfrac{1}{2}\) ) ( 1- \(\dfrac{1}{3}\)) ( 1 - \(\dfrac{1}{4}\)) ( 1 - \(\dfrac{1}{5}\)) = \(\dfrac{1}{2}.\dfrac{1}{3}.\dfrac{1}{4}.\dfrac{1}{5}\)
= \(\dfrac{1}{120}\)
Mình ps có 2 câu à ^.^!

a) \(=\dfrac{-5}{12}.\dfrac{2}{7}+\dfrac{7}{12}.-\dfrac{3}{14}\)
\(=-\dfrac{5}{42}-\dfrac{1}{8}\)
= \(-\dfrac{41}{168}\)
b) \(=\dfrac{2.\left(-13\right).9.10}{\left(-3\right).4.\left(-5\right).26}\)
\(=\dfrac{1.1.3.\left(-2\right)}{\left(-1\right).2.1.\left(-2\right)}=\dfrac{3}{\left(-1\right).2}\)
\(=-\dfrac{3}{2}\)

a) Để phân số \(\dfrac{3}{n-2}\) là số nguyên thì n - 2 \(⋮\) 3
\(\Rightarrow\) n - 2 \(\in\) Ư(3)
\(\Rightarrow\) n - 2 \(\in\){3; -3; 1;-1}
n \(\in\){5; -1; 3; 2}
c) \(\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+......+\dfrac{1}{28.29}\)
\(=\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+.....+\dfrac{1}{29}-\dfrac{1}{30}\)
\(=\dfrac{1}{3}-\dfrac{1}{30}\)
\(=\dfrac{10}{30}-\dfrac{1}{30}\)
\(=\dfrac{9}{30}\)
=\(\dfrac{3}{10}\)

Bài 2:
a: Để A là số nguyên thì \(x+3-5⋮x+3\)
\(\Leftrightarrow x+3\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{-2;-4;2;-8\right\}\)
b: Để B là số nguyên thì \(x^2-1⋮x+1\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)⋮x+1\)
hay \(x\ne-1\)

a) \(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}.....\dfrac{779}{780}\)\(=\)

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)
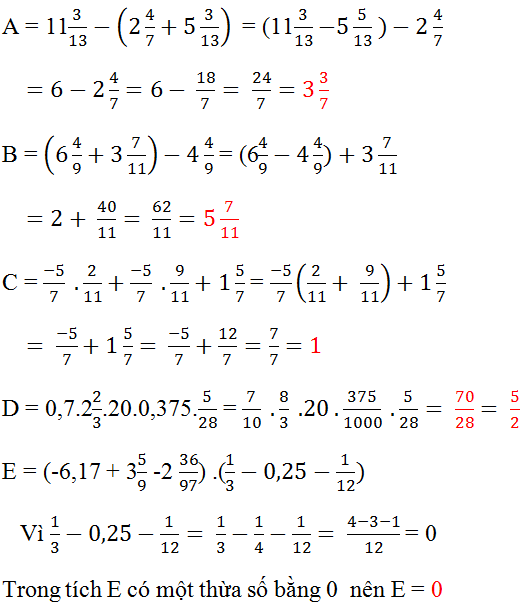
Bài \(13\):
\(C=\dfrac{3}{\left(1\cdot2\right)^2}+\dfrac{5}{\left(2\cdot3\right)^2}+\dfrac{7}{\left(3\cdot4\right)^2}+...+\dfrac{2n+1}{\left[n\left(n+1\right)\right]^2}\)
\(=\dfrac{3}{1\cdot4}+\dfrac{5}{4\cdot9}+\dfrac{7}{9\cdot16}+...+\dfrac{n^2+2n+1-n^2}{n^2\left(n+1\right)^2}\)
\(=\dfrac{4-1}{1\cdot4}+\dfrac{9-4}{4\cdot9}+\dfrac{16-9}{9\cdot16}+...+\dfrac{\left(n+1\right)^2-n^2}{n^2\left(n+1\right)^2}\)
\(=\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+...+\dfrac{1}{n^2}-\dfrac{1}{\left(n+1\right)^2}\)
\(=1-\dfrac{1}{\left(n+1\right)^2}=\dfrac{n\left(n+2\right)}{\left(n+1\right)^2}\)
Bài \(10\):
\(B=\dfrac{5}{2\cdot1}+\dfrac{4}{1\cdot11}+\dfrac{3}{11\cdot2}+\dfrac{1}{2\cdot15}+\dfrac{13}{15\cdot4}\)
\(=7\left(\dfrac{5}{2\cdot7}+\dfrac{4}{7\cdot11}+\dfrac{3}{11\cdot14}+\dfrac{1}{14\cdot15}+\dfrac{13}{15\cdot28}\right)\)
\(=7\left(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{15}+\dfrac{1}{15}-\dfrac{1}{28}\right)\)
\(=7\left(\dfrac{1}{2}-\dfrac{1}{28}\right)=7\cdot\dfrac{13}{28}=\dfrac{13}{4}\)