DN
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
23 tháng 6 2016
a)\(234^{5^{6^7}}=234^{210}\)=...6
-Lũy thừa mà cơ số có tận cùng là 4, số mũ là số chẵn thì tận cùng của lũy thừa đó là 6
b) \(579^{6^{7^5}}=579^{210}\)=...1
-Lũy thừa mà cơ số có tận cùng là 4, số mũ là số chẵn thì tận cùng của lũy thừa đó là 1
22 tháng 8 2019
a) \(3^{2018}=3^{4.504}.3^2=...1.9=...9\)
Vậy chữ số tận cùng là 9
b) \(2^{1000}=2^{4.250}=...6\)
Vậy chữ số tận cùng là 6
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
21 tháng 2 2024
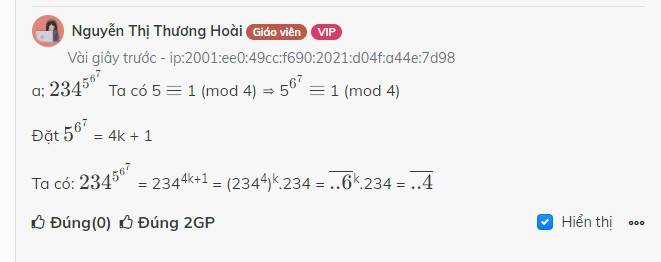
a; \(234^{5^{6^7}}\) Ta có 5 \(\equiv\) 1 (mod 4) ⇒ 5\(^{6^7}\) \(\equiv\) 1 (mod 4)
Đặt \(5^{6^7}\) = 4k + 1
Ta có: \(234^{5^{6^7}}\) = 2344k+1 = (2344)k.234 = \(\overline{..6^{ }}\)k.234 = \(\overline{..4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
21 tháng 2 2024
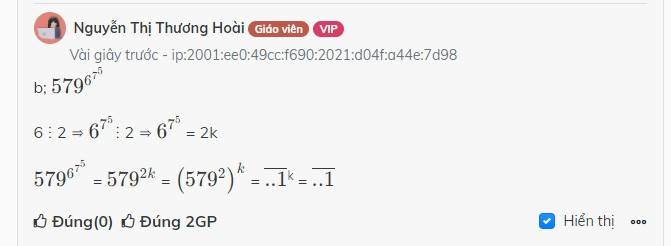
b; \(579^{6^{7^5}}\)
6 ⋮ 2 ⇒ \(6^{7^5}\)⋮ 2 ⇒ \(6^{7^5}\) = 2k
\(579^{6^{7^5}}\) = \(579^{2k}\) = \(\left(579^2\right)^k\) = \(\overline{..1}\)k = \(\overline{..1}\)
21 tháng 12 2018
a) C/m P chia hết cho 3:
\(P=1+2^2+2^3+2^4+...+2^{119}\)
\(P=2^0+2^2+2^3+2^4+...+2^{119}\)
\(P=2^0+2.\left(2^1+2^2+2^3+...+2^{118}\right)\)
Giải thích:
2^2 = 2.2
2^3 = 2.2.2
...
Vậy nếu lấy 1 số 2 làm thừa số chung:
2^2 lấy 1 số 2 con 1 số 2 (2^2 : 2 = 2^1)
2^3 lấy 1 số 2 còn 2 số 2 (2^3 : 2 = 2^2)
2^4 lấy 1 số 2 còn 3 số 2 (2^4 : 2 = 2^3)
...
Tiếp:
Mới nghĩ ra tới đây
Lát làm tiếp
A
0
1 tháng 1 2019
p = 1 + 2 + 2^2 + 2^3 + ... + 2^119
=(1 + 2 + 2^ 2 ) + ( 2^3 + 2^4 + 2^5 ) + ... +(2^117 +2^118+2^119)
= (1 + 2 + 2^ 2 ).1 + 2^3(1+2+2^2) + ...+2^117(1 + 2 + 2^2)
= 7 . 1 + 2^3.7+...+2^117 . 7 = 7 (1 +2^3 + 2^117) \(⋮7\)
1 tháng 1 2019
c, P = 1 + 2 + 2^2 + ... + 2^119
2P = 2 + 2^2 + 2^3 + ... + 2^120
P = 2^120 - 1 = (....6) - 1 = (...5)
giúp mình đi. xin đó
Ta thấy quy luật của các chữ số tận cùng là :
4^1 là 4
4^2 là 6
4^3 là 4
⇒ 4 mũ số lẻ có chữ số tận cùng là 4, 4 mũ số chẵn có chứ số tận cùng là 6
⇒ 5^n luôn có chữ số tận cùng là 5 nên là số lẻ
Vậy 34^5^2018 có chữ số tận cùng là 4.
Đ/S : 4
CHÚC BẠN HỌC TỐT !