CM: x = \(\sqrt[3]{3+\sqrt{9+\dfrac{125}{7}}}-\sqrt[3]{-3+\sqrt{9+\dfrac{125}{7}}}\) là số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Từ giả thiết : \(\dfrac{1}{a}+\dfrac{1}{b}\text{=}\dfrac{1}{c}\)
\(\Rightarrow2ab\text{=}2bc+2ca\)
\(\Rightarrow2ab-2bc-2ca\text{=}0\)
Ta xét : \(\left(a+b-c\right)^2\text{=}a^2+b^2+c^2+2ab-2bc-2ca\)
\(\text{=}a^2+b^2+c^2\)
Do đó : \(A\text{=}\sqrt{a^2+b^2+c^2}\text{=}\sqrt{\left(a+b-c\right)^2}\)
\(\Rightarrow A\text{=}a+b-c\)
Vì a;b;c là các số hữu tỉ suy ra : đpcm
b) Đặt : \(a\text{=}\dfrac{1}{x-y};b\text{=}\dfrac{1}{y-x};c\text{=}\dfrac{1}{z-x}\)
Do đó : \(\dfrac{1}{a}+\dfrac{1}{b}\text{=}\dfrac{1}{c}\)
Ta có : \(B\text{=}\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
Từ đây ta thấy giống phần a nên :
\(B\text{=}a+b-c\)
\(B\text{=}\dfrac{1}{x-y}+\dfrac{1}{y-z}-\dfrac{1}{z-x}\)
Suy ra : đpcm.
Mình bổ sung đề phần b cần phải có điều kiện của x;y;z nha bạn.

😉 Các bạn nhanh tay tham gia ở đây https://www.facebook.com/olm.vn để giật giải thưởng siêu to khổng lồ nha 😁
1 con gấu là: 36 : 3 = 12
1 cái bánh là: ( 26 - 12 ) : 2 = 7
1 Chùm nho là : (15 - 7 ) : 2 = 4
1 con gấu - 1 cái bánh + 1chùm nho
hay: 12 - 7 + 4 = 9

\(\sqrt{\left(4-3\sqrt{2}\right)^2}=\left|4-3\sqrt{2}\right|=3\sqrt{2}-4\)
\(\sqrt{\left(2+\sqrt{5}\right)^2}=\left|2+\sqrt{5}\right|=2+\sqrt{5}\\ \sqrt{\left(4+\sqrt{2}\right)^2}=\left|4+\sqrt{2}\right|=4+\sqrt{2}\)
\(\sqrt{6-2\sqrt{5}}=\sqrt{\sqrt{5^2}-2\sqrt{5}+1}=\sqrt{\left(\sqrt{5}-1\right)^2}=\left|\sqrt{5}-1\right|=\sqrt{5}-1\\ \sqrt{7+4\sqrt{3}}=\sqrt{\sqrt{3^2}+2.2\sqrt{3}+2^2}=\sqrt{\left(\sqrt{3}+2\right)^2}=\left|\sqrt{3}+2\right|=\sqrt{3}+2\\ \sqrt{12-6\sqrt{3}}=\sqrt{\sqrt{3^2}-2.3\sqrt{3}+3^2}=\sqrt{\left(\sqrt{3}-3\right)^2}=\left|\sqrt{3}-3\right|=3-\sqrt{3}\)
\(\sqrt{17+12\sqrt{2}}=\sqrt{\left(2\sqrt{2}\right)^2+2.2\sqrt{2}.3+3^2}=\sqrt{\left(2\sqrt{2}+3\right)^2}=\left|2\sqrt{2}+3\right|=2\sqrt{2}+3\)
\(\dfrac{\sqrt{2}-\sqrt{11+6\sqrt{2}}}{\sqrt{6+2\sqrt{5}}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{\sqrt{2^2}+2.3\sqrt{2}+3^2}}{\sqrt{\sqrt{5^2}+2\sqrt{5}+1}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{\left(\sqrt{2}+3\right)^2}}{\sqrt{\left(\sqrt{5}+1\right)^2}-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\left|\sqrt{2}+3\right|}{\left|\sqrt{5}+1\right|-\sqrt{5}}\\ =\dfrac{\sqrt{2}-\sqrt{2}-3}{\sqrt{5}+1-\sqrt{5}}\\ =-3\)
\(\sqrt{6+2\sqrt{4-2\sqrt{3}}}=\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}=\sqrt{6+2\left|\sqrt{3}-1\right|}=\sqrt{6+2\sqrt{3}-2}=\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\left|\sqrt{3}+1\right|=\sqrt{3}+1\)

b) Xét phương trình 2 có
(1-x2 )/(1+xy)2 - (x+y)2 - y2 =1
=>(1-x2)/1+2xy+x2y2-x2-2xy-y2 -y2=1
=>(1-x2) /(1-x2 )-y2(1-x2) -y2 =1
=>(1-x2)/(1-x2)(1-y2) -y2=1
=>1/(1-y2) -y2=1
=>1=(1-y2)2
=>1=1-2y2+y4
=>y4-2y2=0
=>y2(y2-2)=0
=>y=0
y2-2=0
=> y=+√2
=> y=-√2
Thay y vào phương trình 1 là ra x
à nhầm ... sửa lại dòng 6
=> 1/(1-y2) - y2=1
=> 1/(1-y2)=1+y2
=> 1=1-y4
=> y=0
=>x=3
=> x=-3

\(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+3y^3=2023\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+7\right)\right]\left[\left(x+3\right)\left(x+5\right)\right]+3y^3=2023\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)+3y^3=2023\) (*)
Đặt \(x^2+8x+11=t\left(t\inℤ;t\ge-5\right)\), pt (*) trở thành \(\left(t-4\right)\left(t+4\right)+3y^3=2023\)
\(\Leftrightarrow t^2-16+3y^3=2023\)
\(\Leftrightarrow t^2+3y^3=2039\) (1)
Xét pt (1), dễ thấy \(t^2\equiv0\left(mod3\right)\) hoặc \(t^2\equiv1\left(mod3\right)\), lại có \(3y^3\equiv0\left(mod3\right)\) nên \(VT\equiv0\left(mod3\right)\) hoặc \(VT\equiv1\left(mod3\right)\). Nhưng \(VP=2039\equiv2\left(mod3\right)\), điều này có nghĩa là (1) vô nghiệm.
Vậy phương trình đã cho không thể có nghiệm nguyên.
(x+1)(x+3)(x+5)(x+7)+3y3=2023
⇔[(�+1)(�+7)][(�+3)(�+5)]+3�3=2023⇔[(x+1)(x+7)][(x+3)(x+5)]+3y3=2023
⇔(�2+8�+7)(�2+8�+15)+3�3=2023⇔(x2+8x+7)(x2+8x+15)+3y3=2023 (*)
Đặt �2+8�+11=�(�∈Z;�≥−5)x2+8x+11=t(t∈Z;t≥−5), pt (*) trở thành (�−4)(�+4)+3�3=2023(t−4)(t+4)+3y3=2023
⇔�2−16+3�3=2023⇔t2−16+3y3=2023
⇔�2+3�3=2039⇔t2+3y

a. Khoảng cách từ vật đến thấu kính lớn hơn tiêu cự của thấu kính (d > f)
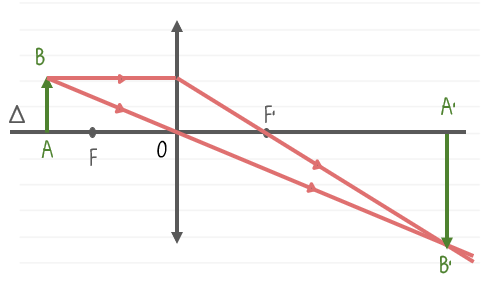
Khi vật đặt ngoài khoảng tiêu cự, ảnh thật ngược chiều với vật.
b.. Khoảng cách từ vật đến thấu kính nhỏ hơn tiêu cự của thấu kính (d < f).
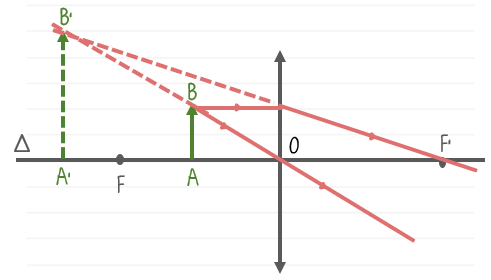
Khi vật đặt trong khoảng tiêu cự, ảnh ảo cùng chiều với vật và lớn hơn vật.


Có vẻ như là đề hơi sai á bạn. Bạn xem lại đề nha.