Cho 2 đa thức: \(N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\)
\(M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\)
a) Tính \(N\left(x\right)-M\left(x\right)\)
b) Tính \(M\left(x\right)+N\left(x\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
30 tháng 5 2022
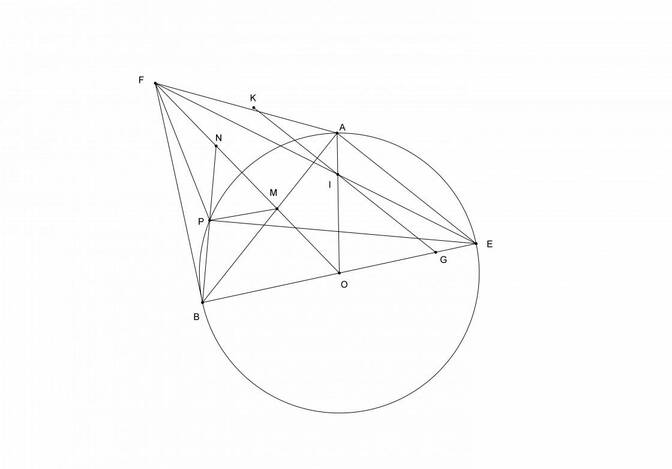
a. Tứ giác AOBF nội tiếp vì có $\angle OAF=\angle OBF=90^o$
b. Chú ý rằng $OF\perp AB$ nên $OF\parallel AE$, ta biến đổi tỉ số bằng định lý Thales:
\(\dfrac{IK}{OF}=\dfrac{AK}{AF}=\dfrac{EG}{EO}=\dfrac{IG}{OF}\), vậy $IK=IG$
c. Nếu mình không nhầm thì PM không vuông NB, vì khi đó $M,P,E$ thẳng hàng, bạn có thể kiểm tra hình vẽ của mình :c
24 tháng 5 2022
a, Thay m = -1 vào phương trình trên ta được
x2+4x−5=0x2+4x−5=0
Ta có : Δ=16+20=36Δ=16+20=36
x1=−4−62=−5;x2=−4+62=1x1=−4−62=−5;x2=−4+62=1
Vậy với m = -1 thì x = -5 ; x = 1
b, Vì x = 2 là nghiệm của phương trình trên nên thay x = 2 vào phương trình trên ta được :
4+8+3m−2=0⇔3m=−10⇔m=−1034+8+3m−2=0⇔3m=−10⇔m=−103
Vậy với x = 2 thì m = -10/3
c, Để phương trình có 2 nghiệm phân biệt thì Δ>0Δ>0hay
16−4(3m−2)=16−12m+8
NM
0
23 tháng 5 2022
Rõ ràng các góc $\angle AOD,\angle BOC $ được đề cập là các góc không lớn hơn $180^o$.
Khi đó ta thấy rằng $\angle AOD,\angle BOC$ là hai góc đối đỉnh nên $\angle AOD=\angle BOC$, từ đó kết hợp giả thiết ta thu được $2\angle AOD=100^o$ hay $\angle AOD=\angle BOC=50^o$
Khi đó $\angle BOD=\angle AOC=180^o-\angle 50^o=130^o$
AH
Akai Haruma
Giáo viên
20 tháng 5 2022
Lời giải:
Giả sử mỗi người cần 1 phần lương thực/ ngày
120 người, 50 ngày thì có:
$120\times 50\times 1=6000$ (phần lương thực)
Sau 3 ngày thì tiêu hết: $3\times 120\times 1=360$ (phần lương thực)
Số lương thực còn lại: $6000-360=5640$ (phần lương thực)
$5640$ phần lương thực này tiêu hết trong:
$50-3-7=40$ (ngày)
Số người sau khi thêm là: $5640:40:1=141$ (người)
Số người đến thêm: $141-120=21$ (người)
a)
\(\begin{matrix}N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\^-M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\\overline{N\left(x\right)-M\left(x\right)=-3x^4+18x^3-2x^2-4x-1}\end{matrix}\)
b)
\(\begin{matrix}M\left(x\right)=-x^4-9x^3+x^2+9x+\dfrac{4}{3}\\^+N\left(x\right)=-4x^4+9x^3-x^2+5x+\dfrac{1}{3}\\\overline{M\left(x\right)+N\left(x\right)=-5x^4+14x+\dfrac{5}{3}}\end{matrix}\)