Cho a,b,c>0 CM : \(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\le\frac{a}{b}+\frac{b}{c}+\frac{c}{a}-\frac{3}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, ĐK : \(x\ne-1;-2\)
\(\frac{2}{x+1}-\frac{3}{x+2}=\frac{1}{2}\Leftrightarrow\frac{2\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}-\frac{3\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}=\frac{\left(x+2\right)\left(x+1\right)}{\left(x+2\right)\left(x+1\right)}\)
Khử mẫu : \(2x+4-3x-3=x^2+x+2x+2\)
\(\Leftrightarrow-x+1=x^2+3x+2\Leftrightarrow-x^2-4x-1=0\)
giải delta nốt nhé !
b;c tương tự


\(\text{áp dụng định lý viet ta có: }\)
\(x_1+x_2=2k;x_1x_2=2k^2+\frac{4}{k^2}-5\)
\(\Rightarrow E=4k^2\left(2k^2+\frac{4}{k^2}-5\right)=8k^4-20k^2+16\)
ta tìm min và max cuả
\(2k^4-5k^2+4\)
hay min và max của \(2k^4-5k^2\text{ thấy ngay: }max_{2k^4-5k^2}=\text{ vô hạn}\)
\(8\left(2k^4-5k^2\right)=16k^4-40k^2=\left(4k^2-5\right)^2-25\ge-25\)
dấu bằng bạn tự tìm


\(5\overrightarrow{IA}-7\overrightarrow{IB}-\overrightarrow{IC}=0\Leftrightarrow5\left(\overrightarrow{GA}-\overrightarrow{GI}\right)-7\left(\overrightarrow{GB}-\overrightarrow{GI}\right)-\left(\overrightarrow{GC}-\overrightarrow{GI}\right)=0\)
\(\Leftrightarrow3\overrightarrow{GI}=-5\overrightarrow{GA}+7\overrightarrow{GB}+\overrightarrow{GC}=-6\overrightarrow{GA}+6\overrightarrow{GB}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=0\right)\)
\(\Leftrightarrow\overrightarrow{GI}=2\left(\overrightarrow{GB}-\overrightarrow{GA}\right)=2\overrightarrow{AB}\)\(\Leftrightarrow GI//AB\Rightarrow\frac{OA}{OI}=\frac{AB}{GI}=\frac{1}{2}\)
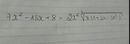
BĐT cần chứng minh tương đương với:
\(\frac{a}{b}-\frac{a}{b+c}+\frac{b}{c}-\frac{b}{c+a}+\frac{c}{a}-\frac{c}{a+b}\ge\frac{3}{2}\)
\(\Leftrightarrow\frac{ac}{b\left(b+c\right)}+\frac{ba}{c\left(c+a\right)}+\frac{cb}{a\left(a+b\right)}\ge\frac{3}{2}\)
Ta có:
\(\frac{ac}{b\left(b+c\right)}+\frac{ba}{c\left(c+a\right)}+\frac{cb}{a\left(a+b\right)}\)
\(=\frac{a^2c^2}{abc\left(b+c\right)}+\frac{b^2a^2}{abc\left(c+a\right)}+\frac{c^2b^2}{abc\left(a+b\right)}\)
\(\ge\frac{\left(ab+bc+ca\right)^2}{abc\left(a+b\right)+abc\left(b+c\right)+abc\left(c+a\right)}\)
\(=\frac{\left(ab+bc+ca\right)^2}{2abc\left(a+b+c\right)}\)
Bất đẳng thức cần chứng minh sẽ đúng nếu ta chứng minh được \(\frac{\left(ab+bc+ca\right)^2}{abc\left(a+b+c\right)}\ge3\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\)
Đặt \(ab=x,bc=y,ca=z\)suy ra ta cần chứng minh
\(\left(x+y+z\right)^2\ge3\left(xy+yz+zx\right)\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2yz+2zx\ge3xy+3yz+3zx\)
\(\Leftrightarrow x^2+y^2+z^2\ge xy+yz+zx\)(đúng)
Vậy bất đẳng thức ban đầu là đúng.
Dấu \(=\)xảy ra khi \(a=b=c\).