(Bài 49 SGK toán 9 tr.87) Dựng tam giác ABC, biết BC = 6 cm, \(\widehat{A}=40^\circ\) và đường cao AH = 4cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A B C D I E K
Ta có :
\(\frac{KC}{sin\widehat{CAK}}=\frac{R\sqrt{2}}{sin\widehat{AKC}}=\frac{R\sqrt{2}}{sin\widehat{AED}}=\frac{AE}{sin\widehat{ADE}}=\frac{AE}{sin\widehat{BIE}}=\frac{AE}{sin\widehat{AIE}}=\frac{3R}{\sqrt{2}}\)
\(\Rightarrow sin\widehat{AKC}=\frac{2}{3}\)
\(\Rightarrow AK=\frac{2}{3R}\)
áp dụng định lý Py ta go vào \(\Delta AOK\) ta được
\(AK^2=AO^2+OK^2\)
\(\Rightarrow OK=\sqrt{R^2-\frac{4}{9R^2}}=\sqrt{9R^4-4}\)
\(\Rightarrow DK=OD-OK=R-\sqrt{9R^4-4}\)

O A B C D E
a, vì \(AD\) là tia phân giác của góc \(\widehat{BAC}\) \(\Rightarrow\widehat{BAD}=\widehat{EAC}\)
mà \(\widehat{ABD}=\widehat{ABC}=\widehat{AEC}\)
\(\Rightarrow\Delta ABD~\Delta AEC\) (g-g)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AC}\Leftrightarrow AB.AC=AE.AD\)
b, Ta có :
\(\widehat{EBD}=\widehat{EBC}=\widehat{EAC}=\widehat{BAE}\)
\(\Rightarrow\Delta EBD~\Delta EAB\)(g-g)
\(\Rightarrow\frac{EB}{EA}=\frac{ED}{EB}\Leftrightarrow ED.EA=EB^2\)
a)xét ΔABE và ΔADC có :
BÅE = DÅC (gt)
AEB=ACB=ACD(cùng chắn cung AB)
=>ΔABE≈ΔADC(g.g)
⇒\(\dfrac{AE}{AC}=\dfrac{AB}{AD}\)(hai cạnh t.ứ)
⇒AE.AD=AC.AB
b)Xét ΔBED và ΔAEB có :
góc E chung
góc EBD=gócEAC=gócEAB
⇒ΔBED ≈ ΔAEB(g.g)
⇒\(\dfrac{ED}{EB}=\dfrac{EB}{EA}\)(hai cạnh t.ứ)
⇒ED.EA=EB2

cần hình ib mình mình gửi cho nhé =)
a)
Vì (O) và (O′) cắt nhau tại hai điểm A và B nên OO′ vuông AB ( định lý )
- Xét tam giác ADC
Có OO′ là đường trung bình ( vì O là trung điểm AC , O′ là trung điểm của AD)
Nên => OO′ // CD
=> AB vuông CD ( Quan hệ từ vuông góc đến song song )
Xét tam giác ADC
Có AC = AD ( vì hai đường tròn (O) và (O′) có cùng bán kính )
=> Tam giác ACD cân tại A có AB là đường cao nên AB cũng là đường trung tuyến
=> BC = BD hay cung BC = cung BD (vì (O) và (O′) là hai đường tròn bằng nhau )
b) Xét đường tròn (O′) có A , E , D cùng thuộc đường tròn và AD là đường kính nên tam giác AED vuông tại E
\(\Rightarrow DE\perp AC\Rightarrow\widehat{DEC}=90^o\)
- Xét \(\Delta DEC\)vuông tại E có B là trung điểm DC ( cmt )
\(\Rightarrow EB=\frac{DC}{2}=BD=EB\)
=> Cung EB = cung BD ( định lý )
Do đó B là điểm chính giữa cung ED

Giải:
Nối M và K
Xét (O) có: \(\hat{AMK}\) là góc nội tiếp chắn cung nhỏ AK
\(\hat{KAB}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung nhỏ AK
\(\Rightarrow\) \(\hat{AMK}\) = \(\hat{KAB}\) ( cùng = 1/2 cung nhỏ AK ) (1)
Xét (O') có : \(\hat{BMK}\) là góc nội tiếp chắn cung nhỏ BK
\(\hat{KBA}\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung nhỏ BK
\(\Rightarrow\) \(\hat{BMK}\) = \(\hat{KBA}\) ( cùng =1/2 cung nhỏ BK ) (2)
Từ (1) và (2) \(\Rightarrow\) \(\hat{AMK}\)+\(\hat{BMK}\)=\(\hat{KAB}\)+ \(\hat{KBA}\)
\(\Leftrightarrow\) \(\hat{AMB}\) = 50° = \(\hat{KAB}\) + \(\hat{KBA}\)
Xét △ KAB có: \(\hat{AKB}\) +(\(\hat{KAB}\) + \(\hat{KBA}\) )= 180° ( Tổng ba góc trong một tam giác)
\(\Leftrightarrow\) \(\hat{AKB}\) + 50° = 180°
\(\Leftrightarrow\)\(\hat{AKB}\) = 180°-50°
\(\Leftrightarrow\)\(\hat{AKB}\) = 130°
Vậy \(\hat{AKB}\) có số đo là 130°

A B C 0 H D
Vẽ đường kính AD và AH⊥BC(H∈BC)AH⊥BC(H∈BC).
Ta có \(\widehat{ACD}\)ACD^ là góc nội tiếp chắn nửa đường tròn ⇒\(\widehat{ACD}\)=900⇒ACD^=900.
Xét ΔABHΔABH và ΔADCΔADC có:
\(\widehat{AHB}\)=\(\widehat{ACD}\)=900AHB^=ACD^=900;
ABH^=ADC^ \(\widehat{ABH}=\widehat{ADC}\)(hai góc nội tiếp cùng chắn cung AC);
⇒ΔABH∼ΔADC(g.g)⇒AHAC=ABAD⇒515=82R⇒2R=24⇔R=12(cm)⇒ΔABH∼ΔADC(g.g)⇒AHAC=ABAD⇒515=82R⇒2R=24⇔R=12(cm)
Trình tự dựng gồm 3 bước:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 40o trên đoạn thẳng BC.
- Dựng đường thẳng xy song song với BC và cách BC một khoảng là 4cm như sau:
Trên đường trung trực d của đoạn thẳng BC lấy đoạn HH' = 4cm (dùng thước có chia khoảng mm). Dựng đường thẳng xy vuông góc với HH' tại H
Gọi giao điểm xy và cung chứa góc là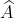 ,
, 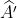 . Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
. Khi đó tam giác ABC hoặc A'BC đều thỏa yêu cầu của đề toán
Cách dựng:
+ Dựng đoạn thẳng BC = 6cm.
+ Dựng cung chứa góc 40º trên đoạn thẳng BC (tương tự bài 46) :
Dựng tia Bx sao cho
Dựng tia By ⊥ Bx.
Dựng đường trung trực của BC cắt By tại O.
Dựng đường tròn (O; OB).
Cung lớn BC chính là cung chứa góc 40º dựng trên đoạn BC.
+ Dựng đường thẳng d song song với BC và cách BC một đoạn 4cm:
Lấy D là trung điểm BC.
Trên đường trung trực của BC lấy D’ sao cho DD’ = 4cm.
Dựng đường thẳng d đi qua D’ và vuông góc với DD’.
+ Đường thẳng d cắt cung lớn BC tại A.
Ta được ΔABC cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 6cm.
+ A ∈ cung chứa góc 40º dựng trên đoạn BC
+ A ∈ d song song với BC và cách BC 4cm
⇒ AH = DD’ = 4cm.
Vậy ΔABC thỏa mãn yêu cầu đề bài.
Biện luận: Do d cắt cung lớn BC tại hai điểm nên bài toán có hai nghiệm hình.