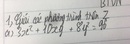
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-3\right)\left(x2-4\right)=0\)
\(\orbr{\begin{cases}x-3=0\\2x-4=0\end{cases}}\)
\(\orbr{\begin{cases}x=3\\2x=4\end{cases}}\)
\(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
Vậy \(x=\left\{2,3\right\}\)

Số lớn nhất có bốn chữ số mà tổng các chữ số của nó đều bằng 3 là 3000
Số bé nhất có bốn chữ số mà tổng các chữ số của nó đều bằng 3 là 1002
Giải
Số lớn nhất có bốn chữ số mà tổng các chữ số của mỗi số đều bằng 3 là : 3000
Số số bé nhất có bốn chữ số mà tổng các chữ số của mỗi số đều bằng 3 là : 1002

Gọi R là độ dài bán kính của đường tròn (O)
Khi đó ta sẽ biểu diễn được: \(\hept{\begin{cases}OH=OC-HC=R-h\\OB=R\end{cases}}\)
Áp dụng định lý Pytago ta có:
\(OH^2+HB^2=OB^2\)
\(\Leftrightarrow\left(R-h\right)^2+a^2=R^2\)
\(\Leftrightarrow R^2-2Rh+h^2+a^2=R^2\)
\(\Leftrightarrow2Rh=h^2+a^2\)
\(\Rightarrow R=\frac{h^2+a^2}{2h}\)
Vậy \(R=\frac{h^2+a^2}{2h}\)
Đặt bán kính đường tròn là x
Ta có: OB=x, OC=x, HC=h, HB=a
⇒OH=OC-HC=x-h
Áp dụng định lí Pi-ta-go vào tam giác vuông OHB:
OB2 = OH2 + HB2
⇔x2=(x - h)2 + a2
⇔2xh =a2 + h2⇔x =\(\dfrac{a^2\text{ +}h^2}{2h}\)

a) Xét 2 TH:
- TH \(P_x,P_y\) nằm về 2 phía của đường kính kẻ qua P ( TH còn lại tương tự)
Kẻ \(OI\perp P_x\) ta có:
\(IP=IE,IA=IB\)
\(\Rightarrow PI-AI=EI-BI\) hay PA=BE ( đpcm)
b) Kẻ \(OK\perp P_y\)
Trong đường tròn \(\left(O;r\right)\), vì AB>CD => OI<OK
Khi đó trong đường tròn \(\Rightarrow PE>PF\)
Theo định lý về mối quan hệ giữa dây và cung , trong đường tròn \(\left(O;R\right)\)
ta có: cung PE > cung PF ( đpcm)
Giải :
a) kẻ OH vuông góc với PE bà AB
⇒ H là trđ PE, AB
hay HP = HE, HA = HB
⇒ HP - HA = HE - HB
⇒ AP = BE.
b) kẻ OK vuông góc với PF
-Xét (O;r) có : AB > CD ( gt)
⇒ OH < OK ( mối liên hệ giữa dây và k/c từ tâm đến dây )
-Xét (O;R) có : OH < OK (cmt )
⇒ PE> PF.

Ta có: \(3x^2+10xy+8y^2=96\)
\(\Leftrightarrow\left(3x^2+6xy\right)+\left(4xy+8y^2\right)=96\)
\(\Leftrightarrow3x\left(x+2y\right)+4y\left(x+2y\right)=96\)
\(\Leftrightarrow\left(3x+4y\right)\left(x+2y\right)=96\) Từ đó ta giải PT nghiệm nguyên ra (Hơi nhiều TH đấy nhé)
Đến phần Ư(96) bạn chỉ cần sử dụng tính chẵn lẻ là sẽ loại bỏ bớt đi 1 số trường hợp rồi