Gọi chiều dài con sông là : \(x\left(m\right)\left(ĐK:x>650\right)\)
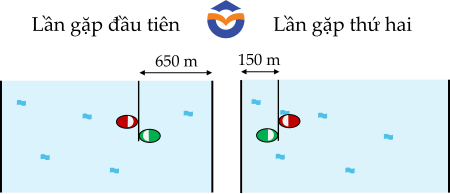
- Trong lần gặp đầu tiên, ca nô màu xanh đi được: $650$ (m) và ca nô màu đỏ đi được: \(x-650\left(m\right)\)
- Do thời gian $2$ ca nô đi được đến khi gặp nhau lần thứ nhất là như nhau
Nên tỉ lệ vận tốc ca nô màu xanh so với ca nô màu đỏ bằng: \(\dfrac{650}{x-650}\)
- Trong lần gặp thứ hai, ca nô màu xanh đi được: \(x+150\left(m\right)\) và ca nô màu đỏ đi được: \(2x-150\left(m\right)\)
- Do thời gian $2$ ca nô đi được đến khi gặp nhau lần thứ hai là như nhau
Nên tỉ lệ vận tốc ca nô màu xanh so với ca nô màu đỏ bằng: \(\dfrac{x+150}{2x-150}\)
Do tỉ lệ vận tốc 2 ca nô luôn không đổi (vì 2 ca nô di chuyển với vận tốc không đổi) nên ta có pt :
\(\dfrac{650}{x-650}=\dfrac{x+150}{2x-150}\)
\(\Rightarrow650\left(2x-150\right)=\left(x-650\right)\left(x+150\right)\\ \Leftrightarrow1300x-97500=x^2-650x+150x-97500\\ \Leftrightarrow1300x-97500=x^2-500x-97500\\ \Leftrightarrow x^2-500x-1300x-97500+97500=0\\ \Leftrightarrow x^2-1800x=0\\ \Leftrightarrow x\left(x-1800\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\left(L\right)\\x=1800\left(TMDK\right)\end{matrix}\right.\)
Vậy chiều dài con sông: $1800$ m.
Tính chiều dài con sông
Người ta quan sát được hai chiếc ca nô đi ngược chiều nhau trên một con sông và di chuyển với vận tốc không đổi theo phương vuông góc với hai bờ sông. Lần đầu tiên hai chiếc ca nô gặp nhau tại vị trí cách bờ sông bên phải 650 m. Khi đến bờ sông phía đối diện, mỗi chiếc cano đều quay đầu ngay lập tức. Một lúc sau, hai cano gặp nhau tại vị trí cách bờ sông bên trái 150 m (Xem hình minh họa).
Hỏi con sông đó dài bao nhiêu? (Bỏ qua chiều dài đoạn đường quay đầu ca nô và chiều dài của mỗi ca nô).
🔹 Các bạn nhấn vào nút 'Gửi bài làm' bên dưới để trình bày lời giải đầy đủ của mình. Tối đa 10 bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra thẻ cào, ngày VIP, phần quà, ... chi tiết tại trang web: shop.olm.vn
🔹 Cuộc thi kết thúc vào 11:00 ngày 15/03/2024. Câu đố tiếp theo sẽ lên vào trước 17 giờ cùng ngày.
