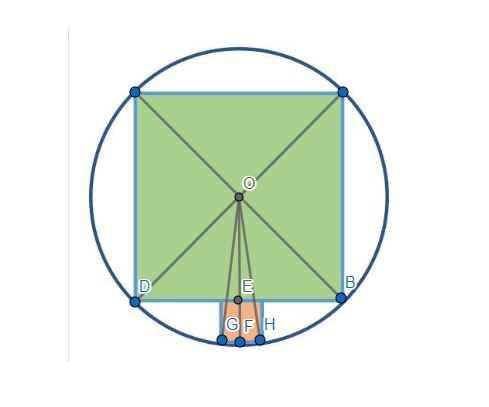
Gọi a là độ dài hình vuông màu xanh, diện tích hình vuông xanh bằng \(S_{xanh}=a^2\)
Bán kính hình tròn bằng \(\dfrac{\sqrt{a^2+a^2}}{2}=\dfrac{a}{\sqrt{2}}\)
Gọi b là độ dài hình vuông màu cam, diện tích hình vuông cam bằng \(S_{cam}=b^2\)
O là tâm hình tròn; E là trung điểm của DB
Ta có OE \(\perp\) DB (tam giác ODB cân nên đường trung tuyến OE cũng là đường cao)
=> OE = \(\dfrac{a}{2}\)
Kéo dài OE cắt GH tại F
Vì DB song song với GH nên OF vuông góc với GH tại F
Tam giác OGH cân tại O (OG = OH bằng bán kính hình tròn)
Suy ra OF cũng là đường trung tuyến của tam giác OGH => FG = \(\dfrac{b}{2}\)
Áp dụng định lí pitago vào tam giác vuông OFG ta có:
(OE + EF)2 + FG2 = OG2
\(\Leftrightarrow\left(\dfrac{a}{2}+b\right)^2+\left(\dfrac{b}{2}\right)^2=\left(\dfrac{a}{\sqrt{2}}\right)^2\\ \Leftrightarrow\dfrac{a^2}{4}+ab+b^2+\dfrac{b^2}{4}=\dfrac{a^2}{2}\\ \Leftrightarrow\dfrac{5b^2}{4}+ab-\dfrac{a^2}{4}=0\\ \dfrac{5}{4}+\dfrac{a}{b}-\dfrac{1}{4}\left(\dfrac{a}{b}\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{a}{b}=-1Loại\\\dfrac{a}{b}=5\end{matrix}\right.\)
\(\Rightarrow\dfrac{a^2}{b^2}=\dfrac{S_{xanh}}{S_{cam}}=25.\)đpcm
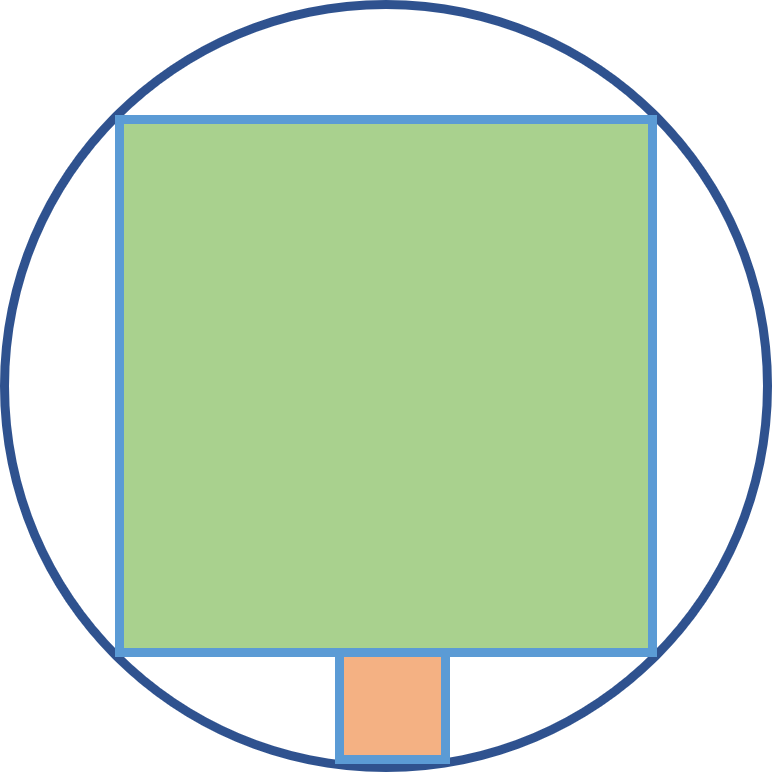
Cho hình vẽ. Tính tỉ số diện tích hình vuông màu xanh và hình vuông màu cam.
------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra tiền mặt, thẻ cào, ngày VIP, ... . Giải thưởng sẽ được công bố vào Thứ Sáu ngày 23/9/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 23/9/2022.

