Có nhiều lời giải hay cho bài toán này, OLM xin giới thiệu lời giải xuất sắc của 3 bạn.
1. Lời giải của Tạ Duy Hưng
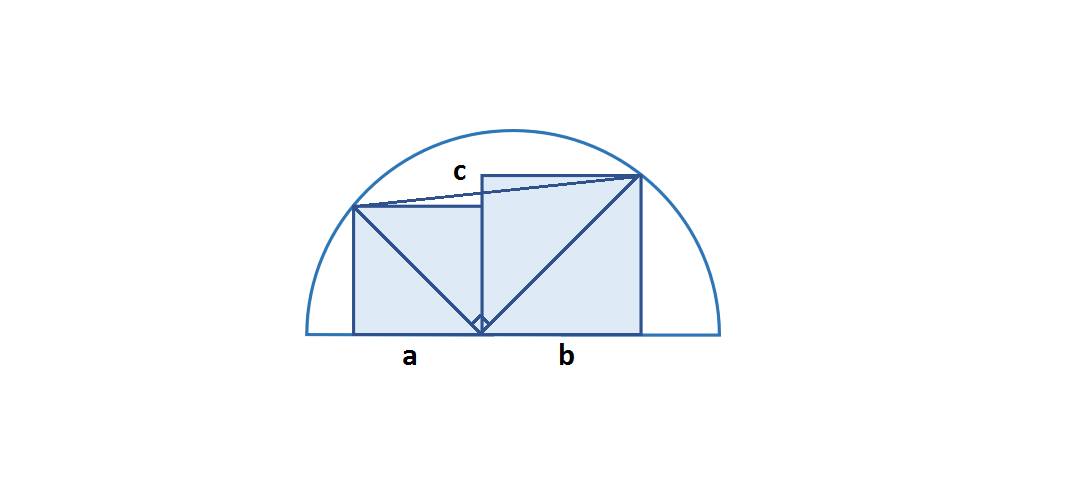
Gọi độ dài cạnh của hình vuông bên trái là a, hình vuông bên phải là b.
Vẽ 2 đường chéo của 2 hình vuông này. Ta nhận thấy góc mà hai đường chéo này tạo ra là góc vuông.
Áp dụng định lí Pytago, ta tính độ dài đường chéo của hình vuông bên trái bằng: \(\sqrt{a^2+a^2}=a\sqrt{2}\)
độ dài đường chéo của hình vuông bên trái bằng:\(\sqrt{b^2+b^2}=b\sqrt{2}\)
Lại áp dụng định lí Pytago, ta tinh được độ dài của đường thẳng có độ dài c bằng:
\(c^2=\left(a\sqrt{2}\right)^2+\left(b\sqrt{2}\right)^2\)
\(\Leftrightarrow c^2=2a^2+2b^2\)(*)
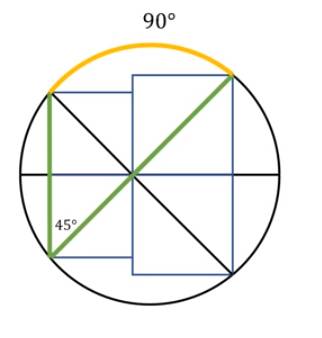
Ta sẽ tìm số đo của cung tròn màu vàng trên hình.
Sao chép một hình y hệt hình ban đầu rồi lật ngược, gắn liền với hình ban đầu tạo thành hình trên.
Ta thấy: số đo của góc nội tiếp màu xanh trên hình bằng 1 nửa góc vuông.
Áp dụng định lý góc nội tiếp ta tính được số đo của cung tròn này bằng 90o.
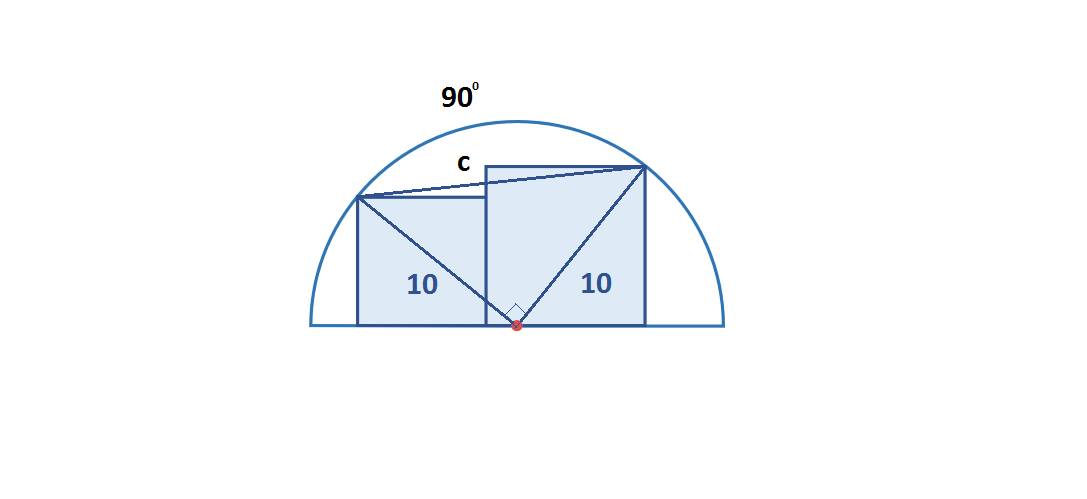
Nối 2 điểm của đoạn thẳng có độ dài c với tâm hình tròn, ta được hình trên.
Vì cung tròn trên bằng 90o nên góc tạo từ 2 đoạn thẳng nối tâm hình tròn với 2 điểm của đoạn thẳng độ dài c cũng bằng 90o.
Áp dụng đinh lý Pytago, ta có:
\(c^2=10^2+10^2=100+100=200\)(**)
Từ (*) và (**) ta có:
\(c^2=2a^2+2b^2=200\)
\(=2\left(a^2+b^2\right)=200\)
\(=a^2+b^2=200:2=100\)
Ta thấy: tổng diện tích 2 hình vuông bằng \(a^2+b^2\) mà \(a^2+b^2=100\) vậy tổng diện tích 2 hình vuông là 100 (đơn vị diện tích)
2. Lời giải của Nguyễn Viết Trung Nhân

Gọi \(OB = c, EB = FE = FD = DB = a, HB = HG = GI = BI = b, OM = r\)
Xét hai tam giác vuông OEF và OIG có: \(r^2 = a^2 + (a+c)^2; r^2 = b^2 + (b-c)^2\)
\(\Rightarrow \sqrt{r^2 - a^2} - a = b - \sqrt{r^2 - b^2} (=c)\)
Bình phương cả hai vế lên, ta có: \(a\sqrt{r^2 - a^2} = b\sqrt{r^2 - b^2}\)
Bình phương hai vế thêm một lần nữa, ta có: \(a^2(r^2 - a^2) = b^2(r^2 - b^2)\)
\(\Rightarrow r^2(a^2 - b^2) = a^4 - b^4\)
\(\Rightarrow r^2(a^2 - b^2) = (a^2 - b^2)(a^2 + b^2)\)
\(\Rightarrow a^2 + b^2 = r^2 = 100\)
Vậy tổng diện tích của hai hình vuông là 100
3. Lời giải của Nguyen Dang Phuc
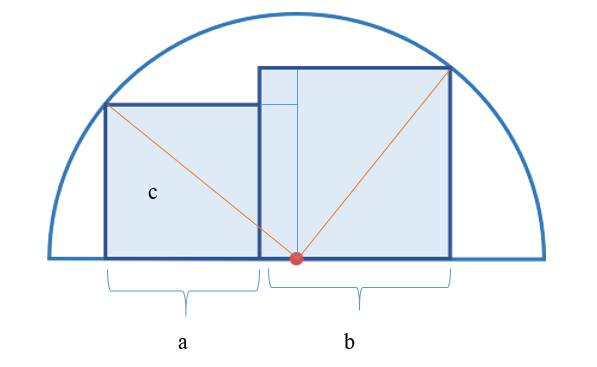
Gọi cạnh của hình vuông nhỏ là a, hình vuông lớn là b. Kẻ thêm các đường như trên, ta được 4 hình tam giác vuông có các cạnh bằng nhau và có chiều cao là a, cạnh đáy là b, cạnh huyền là c. Theo định lý Py-ta-go thì có: c2 = a2 + b2 mà c là đoạn thẳng được kẻ từ tâm nửa vòng tròn đến 1 điểm trên đường tròn nên c2 = 102 = 100 => a2 + b2 = 100. Ta có diện tích của 2 hình vuông = a2 + b2 => diện tích của hình vuông là: 100 (đơn vị diện tích)
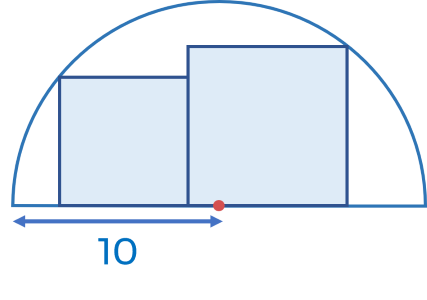
Có hai hình vuông tiếp xúc với nhau và tiếp xúc với nửa đường tròn bán kính 10 như hình vẽ. Tính tổng diện tích hai hình vuông.
------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra tiền mặt, thẻ cào, ngày VIP, ... . Giải thưởng sẽ được công bố vào Thứ Sáu ngày 24/6/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 24/6/2022.





