Lời giải của 🐟 ⋆ 🐇 🎀 𝒩𝑔𝓊𝓎ễ𝓃 Đă𝓃𝑔 𝒩𝒽â𝓃 🎀 🐇 ⋆ 🐟
Cách 1: Từ bài toán, ta phân tích hình ảnh như sau:
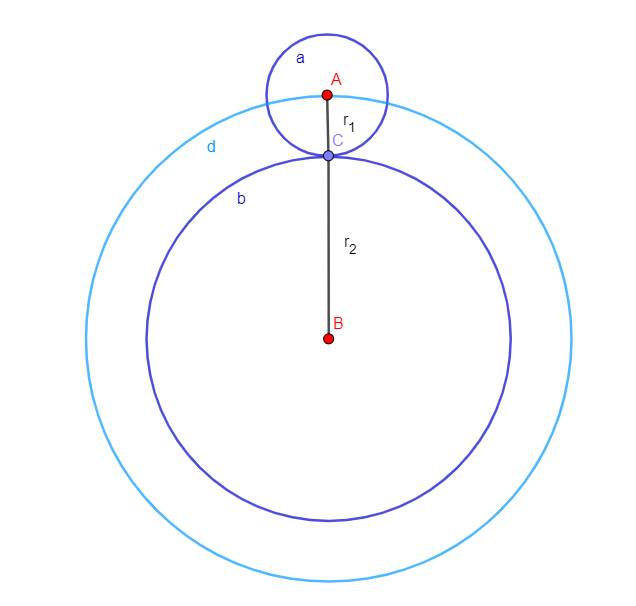
Ta có:
Số vòng mà đường tròn a "lăn" được trên đường tròn b cũng chính là số lần mà tâm A di chuyển được trên đường tròn d (1 lần di chuyển của tâm A trên đường tròn d bằng độ dài đường tròn a).
Mà khoảng cách giữa A và B là tổng bán kính đường tròn a với bán kính đường tròn b (tổng gấp 4 lần bán kính đường tròn a) nên chu vi đường tròn d gấp 4 lần chu vi đường tròn a hay tâm A cần di chuyển 4 lần trên đường tròn d để về lại vị trí cũ.
Mặt khác: đường tròn a cần phải "lăn" 4 lần trên đường tròn b để về lại vị trí cũ.
Vậy đường tròn (A) trên bài toán cần phải "lăn" 4 vòng trên đường tròn (B) để về lại vị trí cũ.
Cách 2: Vì đường kính đường tròn (B) gấp 3 lần đường kính đường tròn (A) nên chu vi đường tròn (B) cũng gấp 3 lần chu vi đường tròn (A).
Ta chia đường tròn (B) thành 3 phần như sau (mỗi phần bằng chu vi đường tròn (A).):
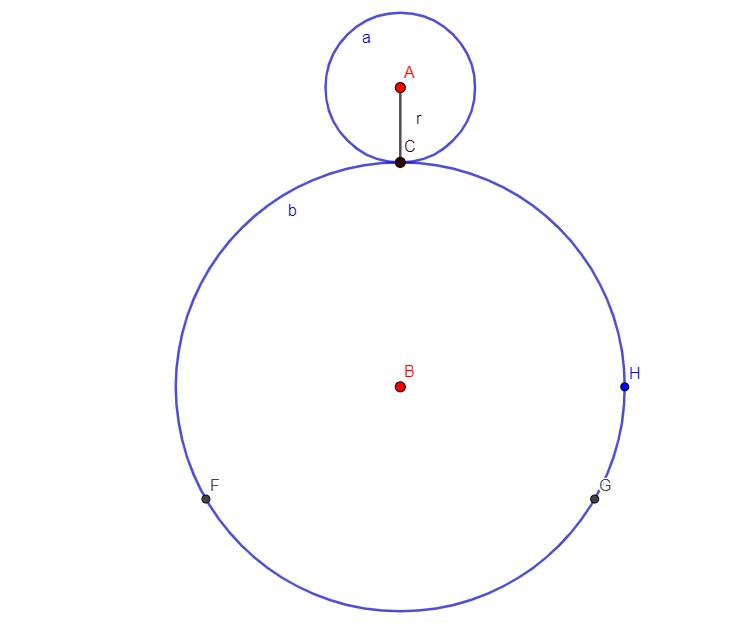
Từ C tới G, khi đường tròn a quay 1 vòng (\(360^o\) theo chiều kim đồng hồ) thì tới điểm H. Từ H, đường tròn a phải quay thêm \(120^o\) (theo chiều kim đồng hồ) nữa mới tới điểm G nên từ C tới G đường tròn a cần quay: \(360^o+120^o=480^o\)
\(\Rightarrow\)Số vòng mà đường tròn a cần quay để về lại vị trí cũ là: \(\dfrac{\left(360\cdot3\right)+\left(120\cdot3\right)}{360}=4\left(vòng\right)\)
Vậy đường tròn (A) trên bài toán cần "lăn" 4 vòng trên đường tròn (B) để về vị trí cũ.
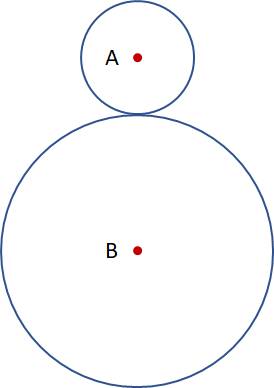
Ở hình vẽ trên, đường tròn (B) có bán kính bằng 3 lần bán kính của đường tròn (A). Hỏi nếu đường tròn (A) "lăn" trên đường tròn (B) thì phải mất bao nhiêu vòng để về vị trí cũ?
Gợi ý: Bài toán này không dễ như bạn nghĩ 😀
-------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra tiền mặt, thẻ cào, ngày VIP, ... . Giải thưởng sẽ được công bố vào Thứ Sáu ngày 20/5/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 20/5/2022.


