Lời giải của 🐟 ⋆ 🐇 🎀 𝒩𝑔𝓊𝓎ễ𝓃 Đă𝓃𝑔 𝒩𝒽â𝓃 🎀 🐇 ⋆ 🐟
Từ bài toán, ta có phân tích bài toán như sau:
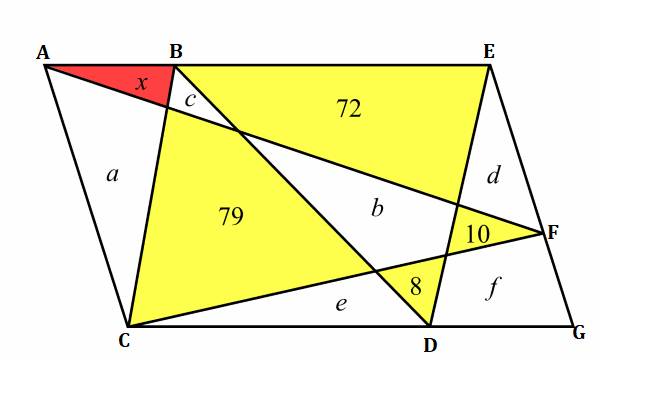
Ta có:
Vì 2 cạnh đáy tam giác ABC, BED có tổng độ dài bằng chiều dài AE của hình bình hành AEGC ( \(AB+BE=AE\) ) và 2 đỉnh hình tam giác ABC, BED ( Đỉnh C và đỉnh D) đều nằm trên chiều dài CG của hình bình hành AEGC nên tổng diện tích 2 hình tam giác ABC, BED sẽ bằng một nửa diện tích hình bình hành AEGC. (1)
Vậy: \(\left(x+a\right)+\left(72+b+8\right)=\dfrac{AEGC}{2}\)
Lại có:
Cạnh đáy hình tam giác AFC là chiều rộng AC của hình bình hành AEGC và đỉnh hình tam giác AFC (Đỉnh F) nằm trên chiều rộng EG của hình bình hành AEGC nên diện tích hình tam giác AFC sẽ bằng một nửa diện tích hình bình hành AEGC.
Từ (1) và (2), ta được:
\(\left(\Delta ABC+\Delta BED\right)=\Delta AFC\)
\(\Rightarrow\left(x+a\right)+\left(72+b+8\right)=a+79+b+10\)
\(\Rightarrow x+72+8=a+79+b+10-a-b\)
\(\Rightarrow x+72+8=79+10\)
\(\Rightarrow x=79+10-72-8\)
\(\Rightarrow x=9\)
Vậy diện tích x của phần màu đỏ sẽ bằng 9 (đơn vị đo diện tích).
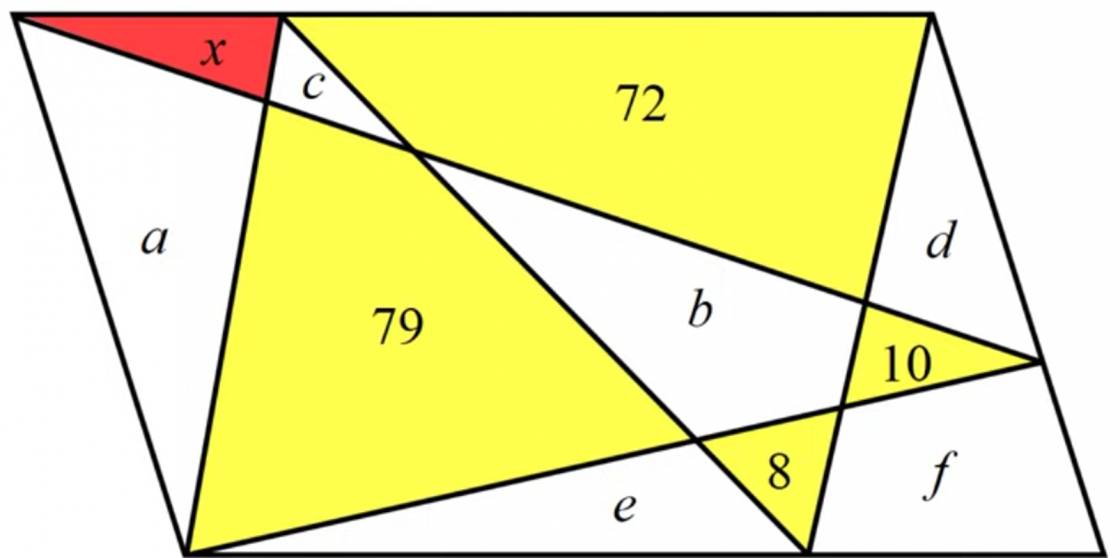
Một hình bình hành được chia thành các phần nhỏ như hình vẽ. Mỗi phần nhỏ có diện tích được cho bằng các số hoặc các chữ. Đố bạn tìm được diện tích $x$ của phần màu đỏ.
-------------------------
Các bạn nhấn vào nút Tham dự bài thi bên dưới để trình bày lời giải đầy đủ của mình. Mười bạn có lời giải hay và sớm nhất sẽ được cộng/thưởng coin của OLM để đổi ra tiền mặt, thẻ cào, ngày VIP, ... . Giải thưởng sẽ được công bố vào Thứ Sáu ngày 13/5/2022. Câu đố tiếp theo sẽ lên mạng vào Thứ Sáu ngày 13/5/2022.

