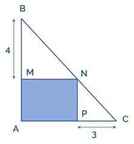
a) Ta có: \(\Delta BMN∽\Delta NPC\Rightarrow\dfrac{BM}{NP}=\dfrac{MN}{PC}\Rightarrow NM.NP=BM.PC=12.\)

Do đó \(S_{AMNP}=NN.NP=12.\)

b) \(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}\left(AM+4\right)\left(AP+3\right).\)

\(\left(AM+4\right)\left(AP+3\right)=AM.AP+3AM+4AP+12=24+3AM+4AP.\)

\(3AM+4AP\overset{\text{BĐT Cô-si}}{\ge}2\sqrt{3AM.4AP}=2\sqrt{12.12}=24.\)

Dấu "=" xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}3AM=4AP\\AM.AP=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AM=4\\AP=3\end{matrix}\right..\)

Vậy diện tích tam giác ABC nhỏ nhất bằng 24 khi AB = 8, AC = 6.