Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Ứng dụng tích phân để tính diện tích hình phẳng SVIP
Cho hàm số y=f(x) xác định và liên tục trên đoạn. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b được tính theo công thức nào?
Cho hàm số y=f(x) và y=g(x) có đồ thị như hình vẽ:
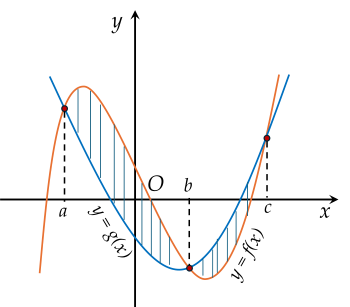
Diện tích S của phần gạch chéo trong hình vẽ trên được tính bằng công thức là
Diện tích hình phẳng (H) được giới hạn bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a,x=b (a<b) (phần gạch chéo như hình vẽ) được tính theo công thức nào?
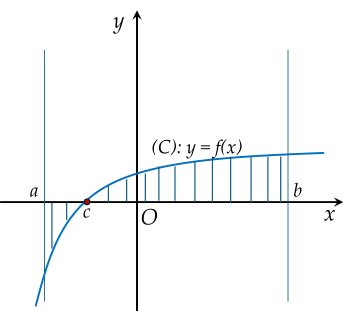
Diện tích S hình phẳng giới hạn bởi các đường y=2x2, y=−1, x=0 và x=1 là
Diện tích hình phẳng giới hạn bởi hai đường y=x2 và y=x là
Cho hình phẳng (D) giới hạn bởi đồ thị của ba hàm số y=f(x), y=g(x), y=h(x) như hình bên dưới:

Diện tích hình phẳng (D) là
Diện tích hình phẳng giới hạn bởi parabol y=x2 và đường thẳng y=3x−2 là
Cho đường thẳng y=x−a (a là tham số thực dương) và đồ thị hàm số y=x. Gọi S1,S2 lần lượt là diện tích hai hình phẳng được gạch chéo trong hình vẽ dưới đây:
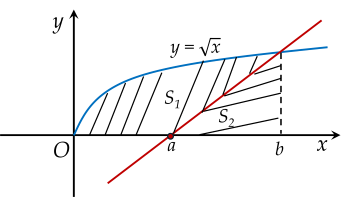
Khi S1=35S2 thì a bằng bao nhiêu?
Trả lời:
Cho đồ thị hàm số y=f(x) và y=g(x) như hình vẽ bên dưới:
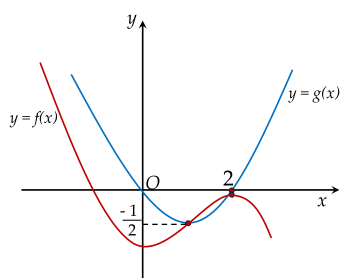
Biết đồ thị của hàm số y=g(x) là một Parabol đỉnh I có tung độ bằng −21 và y=f(x) là một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là x1,x2,x3 thỏa mãn x1.x2.x3=−6. Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số y=f(x) và y=g(x) gần nhất giá trị nguyên nào?
Trả lời:
Cho hàm số y=f(x) liên tục trên đoạn [0;8] và có đồ thị như hình vẽ:
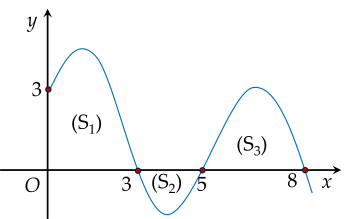
| a) S1=∫03f(x)dx. |
|
| b) S2+S3=∫38f(x)dx. |
|
| c) S1−S2=−∫05f(x)dx. |
|
| d) ∫08f(x)dx>∫58f(x)dx. |
|

Bạn có thể đăng câu hỏi về bài học này ở đây
