Tự luận (3 điểm) SVIP

Hướng dẫn giải:

Gọi số tiền vay ban đầu là ${{u}_{0}}$, tiền trả hàng tháng là $x$, lãi suất hàng tháng là $0,7\%$.

Số tiền còn lại sau $1$ tháng: ${{u}_{1}}={{u}_{0}}1,007-x$ (đồng).

Số tiền còn lại sau $2$ tháng:

${{u}_{2}}={{u}_{1}}1,007-x={{u}_{0}}1,{{007}^{2}}-1,007x-x={{u}_{0}}1,{{007}^{2}}-x(1+1,007 )$ (đồng).

Số tiền còn lại sau $n$ tháng:

${{u}_{n}}={{u}_{0}}1,{{007}^{n}}-x(1+1,007+1,{{007}^{2}}+...+1,{{007}^{n-1}} )$

$={{u}_{0}}1,{{007}^{n}}-x\dfrac{1,{{007}^{n}}-1}{0,007}$ (đồng).

Sau $n$ tháng thì hết nợ $\Rightarrow {{u}_{n}}=0$

$\Leftrightarrow {{u}_{0}}=\dfrac{x(1,{{007}^{n}}-1 )}{0,007.1,{{007}^{n}}}$ (đồng).

Để trả hết nợ thì An cần $10$ tháng và Bình cần $15$ tháng, ta được:

$\dfrac{x(1,{{007}^{10}}-1 )}{0,007.1,{{007}^{10}}}+\dfrac{x(1,{{007}^{15}}-1 )}{0,007.1,{{007}^{15}}}={{2.10}^{8}}$

$\Leftrightarrow x=8\,397\,068,067$ (đồng).

Hướng dẫn giải:

Do $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AD=2a\Rightarrow AB=BC=CD=a$

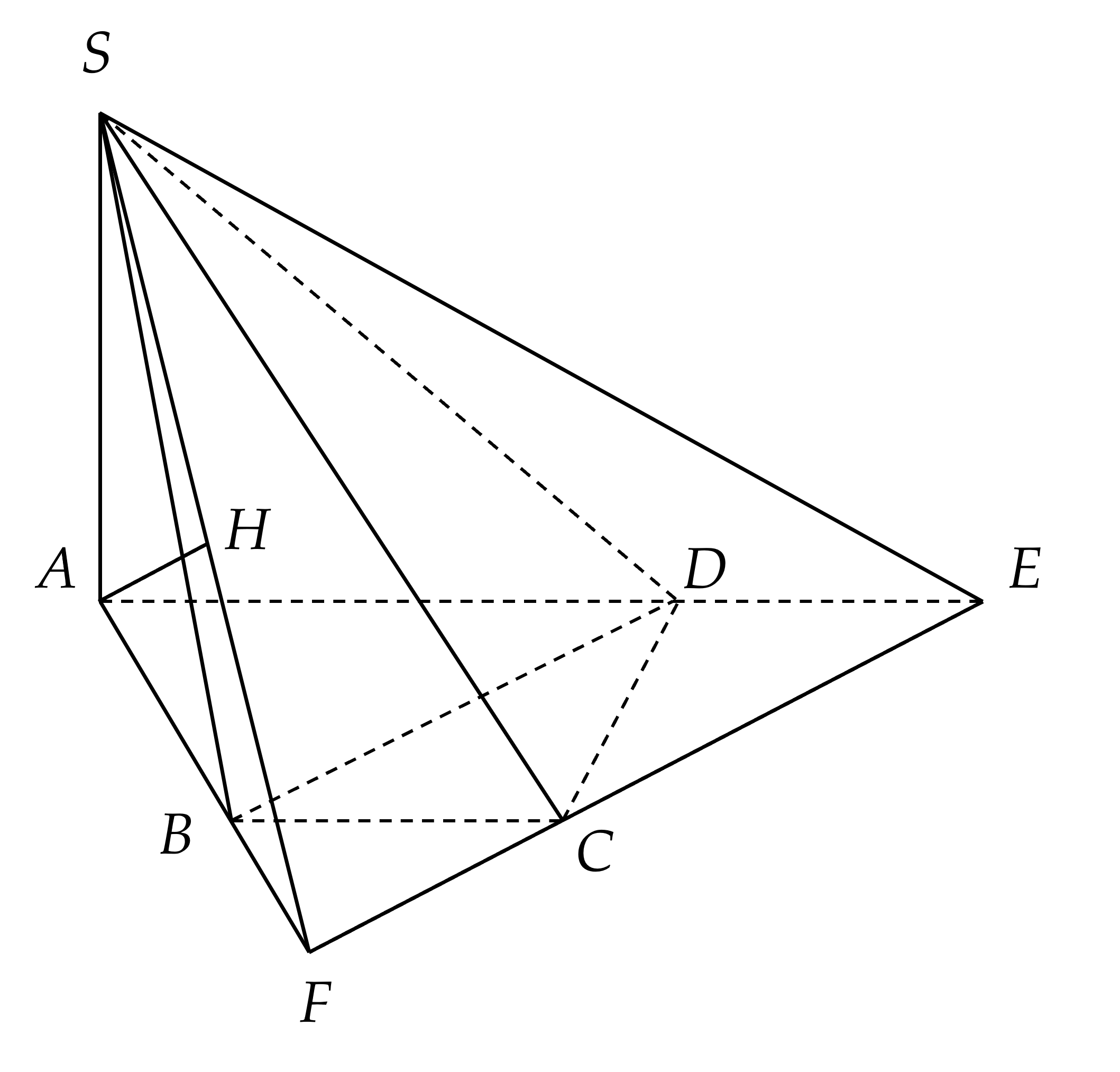
 Kẻ đường thẳng $CE//BD\,\,(E\in AD )$, gọi $F=CE\cap AB\Rightarrow BD//(SEF )$.

Khi đó $d(BD;SC )=d(BD;(SCE ) )=d(D;(SCE ))$

Ta có $BCED$ là hình bình hành nên $DE=BC=a\Rightarrow AE=3a$

Ta có $d(D;(SCE ) )=\dfrac{1}{3}d(A;(SCE ) )$

Ta có $\widehat{ABD}=90^\circ$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow BD\bot AB$

$\Rightarrow EF\bot AB$

$\Rightarrow \left\{ \begin{aligned}& EF\bot SA \\& EF\bot AB \\\end{aligned} \right.\Rightarrow EF\bot (SAB )$

Kẻ $AH\bot SF\Rightarrow \left\{ \begin{aligned}& AH\bot SF \\& AH\bot EF \\\end{aligned} \right.$

$\Rightarrow AH\bot (SEF )\Rightarrow d(A;(SEF ) )=AH$

Ta có $AF=\dfrac{3}{2}AB=\dfrac{3a}{2}=SA$ suy ra tam giác $SAF$ vuông cân tại $A$

$\Rightarrow AH=\dfrac{1}{2}SF$

$=\dfrac{1}{2}\sqrt{SA^2+AF^2}$

$=\dfrac{1}{2}.\dfrac{3a\sqrt{2}}{2}$

$=\dfrac{3a\sqrt{2}}{4}$.

Vậy $d(D;(SCE ))=\dfrac{1}{3}d(A;(SCE ) )=\dfrac{a\sqrt{2}}{4}$.

Hướng dẫn giải:

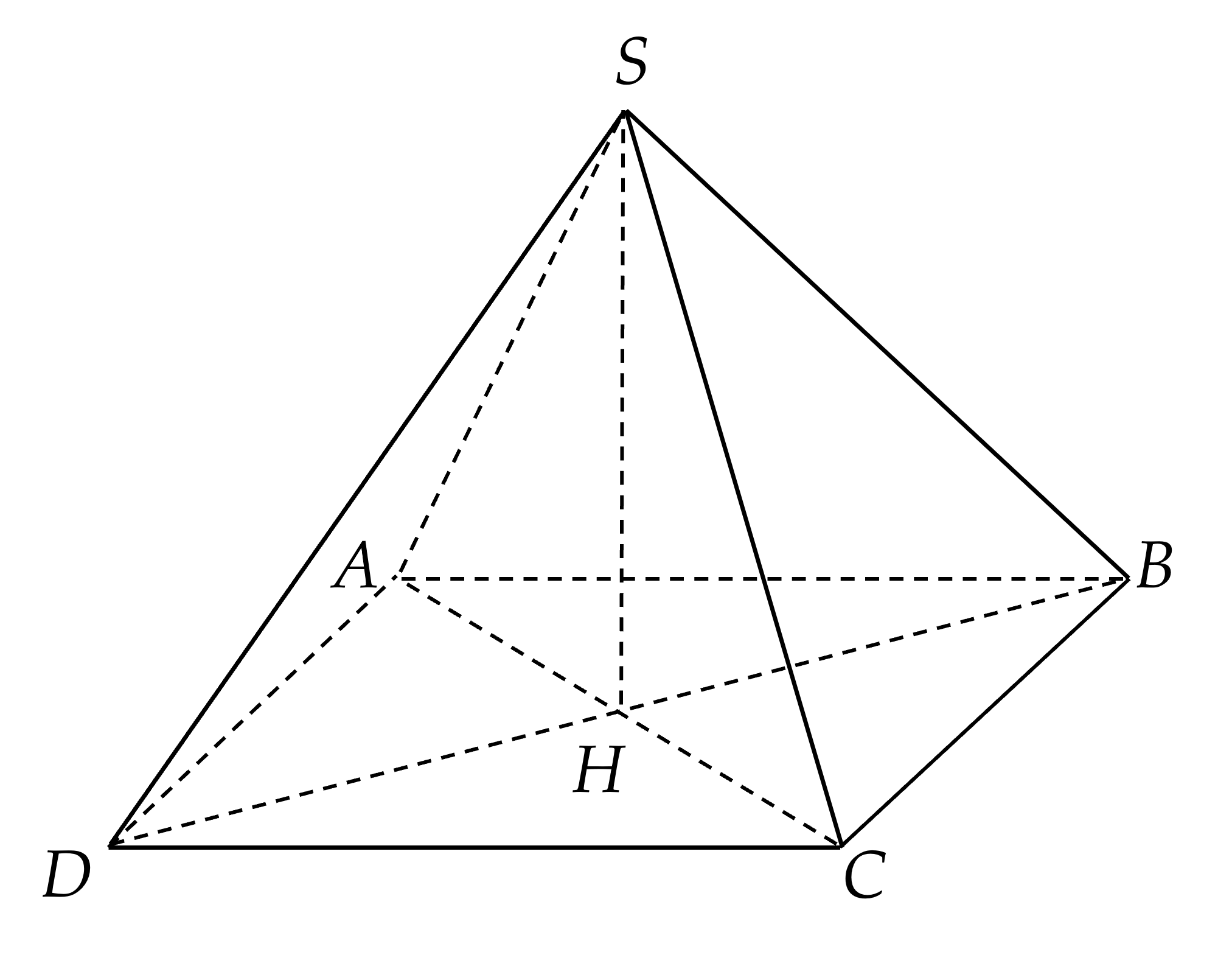
 Gọi $H=AC\cap BD$. Vì $SA=SB=SC=SD$ nên $HA=HB=HC=HD$

$\Rightarrow ABCD$ là hình chữ nhật và $H$ là hình chiếu vuông góc của $S$ xuống $(ABCD )$

Giả sử $AB=a$. Đặt $AD=x$. Khi đó

${{S}_{ABCD}}=ax.$

$AH=\dfrac{AC}{2}=\dfrac{\sqrt{AB^2+BC^2}}{2}=\dfrac{\sqrt{a^2+x^2}}{2}.$

$SH=\sqrt{S{{A}^{2}}-A{{H}^{2}}}=\sqrt{2{{a}^{2}}-\dfrac{{{a}^{2}}+{{x}^{2}}}{4}}=\dfrac{\sqrt{7{{a}^{2}}-{{x}^{2}}}}{2}.$

Ta có

$ {V_{S.ABCD}}=\dfrac{1}{3}.SH.{{S}_{ABCD}}$

$=\dfrac{1}{3}.\dfrac{\sqrt{7{{a}^{2}}-{{x}^{2}}}}{2}.ax$

$=\dfrac{ax\sqrt{7{{a}^{2}}-{{x}^{2}}}}{6}\le \dfrac{1}{6}.a.\dfrac{({{x}^{2}}+7{{a}^{2}}-{{x}^{2}} )}{2}$

$ \Rightarrow {V_{S.ABCD}}\le \dfrac{7{{a}^{3}}}{12}.$

Dấu xảy ra khi $x=\sqrt{7{{a}^{2}}-{{x}^{2}}}$ hay $x=\dfrac{a\sqrt{14}}{2}$.

Vậy thể tích của khối chóp có giá trị lớn nhất là $\dfrac{7{{a}^{3}}}{12}$ khi $x=\dfrac{a\sqrt{14}}{2}$.