Bài học cùng chủ đề
- Trường hợp bằng nhau thứ nhất của hai tam giác
- Trường hợp bằng nhau thứ hai của hai tam giác
- Trường hợp bằng nhau thứ ba của hai tam giác
- Trường hợp đồng dạng thứ nhất của tam giác (c.c.c)
- Trường hợp đồng dạng thứ hai của tam giác (c.g.c)
- Trường hợp đồng dạng thứ ba của tam giác (g.g)
- Trường hợp đồng dạng thứ nhất của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ nhất của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ hai của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ hai của hai tam giác (vận dụng)
- Trường hợp đồng dạng thứ ba của hai tam giác (cơ bản)
- Trường hợp đồng dạng thứ ba của hai tam giác (nâng cao)
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Trường hợp đồng dạng thứ nhất của hai tam giác (cơ bản) SVIP
Cho tam giác ABC có AB=6 cm, AC=9 cm, BC=12 cm và tam giác MNP có NP=8 cm, NM=12 cm, PM=16 cm. Khẳng định nào sau đây đúng?
Cho tam giác MNP có MN=4 cm, MP=5 cm, NP=7 cm và tam giác HIK có HI=8 cm, HK=10 cm, IK=14 cm. Khẳng định nào sau đây đúng?
Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?
Với điều kiện nào sau đây thì ΔABC∽ΔMNP?
Với điều kiện nào sau đây thì ΔMNP∽ΔHIK?
Cho hai hình vẽ:
Khẳng định nào dưới đây đúng?
Cặp tam giác với độ dài các cạnh nào dưới đây đồng dạng với nhau?
Cho các cặp tam giác với độ dài các cạnh như sau. Cặp tam giác nào không đồng dạng với nhau?
Cho các tam giác như trong hình vẽ.
Mỗi khẳng định sau đúng hay sai?
(Nhấp vào dòng để chọn đúng / sai)| Tam giác ABC không đồng dạng với tam giác MNP. |
|
| ΔDEF∽ΔMNP. |
|
| ΔABC∽ΔMNP. |
|
| ΔABC∽ΔDEF. |
|
Cho ΔABC∽ΔA1B1C1. Khẳng định nào sau đây sai?
Cho ΔABC∽ΔMNP biết AB=3 cm, BC=4 cm, MN=6 cm, MP=5 cm. Khi đó
Cho ΔHIK∽ΔMNP biết HK=3 cm, HI=4 cm, MP=9 cm, NP=12 cm. Khi đó
Cho hình vẽ sau.
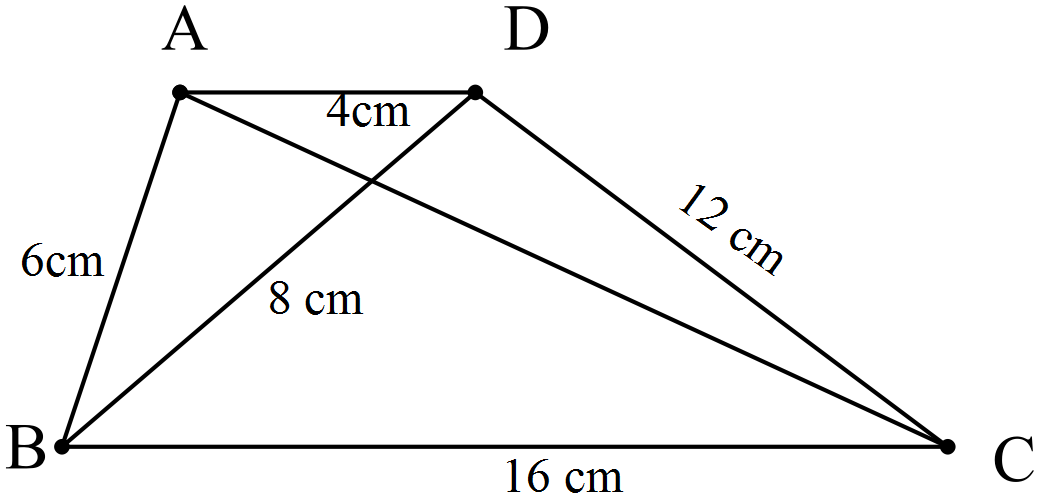
Khẳng định nào dưới đây đúng?

Bạn có thể đăng câu hỏi về bài học này ở đây
