Đề ôn tập và kiểm tra giữa học kì I toán 10 mới nhất

Câu 1 (1đ):

Cho tam giác $ABC$ có $\widehat{A}=45^\circ, \, AB=6, \, \widehat{B}=75^\circ$ . Độ dài cạnh $BC$ bằng

3\sqrt{6}

\dfrac{3}{\sqrt{2}}.

2\sqrt{3}.

2\sqrt{6}.

Câu 2 (1đ):

Giá trị của biểu thức $P=\sin 30^\circ. \cos 60^\circ + \sin 60^\circ. \cos 30^\circ$ là

P=0

.

P=1

.

P=\sqrt{3}

.

P=-\sqrt{3}

.

Câu 3 (1đ):

Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned} & x-2y<0 \\ & x+3y>-2 \\ & y-x<3 \\ \end{aligned} \right.$ chứa điểm nào sau đây?

(0;-1)

.

(-1;0).

(1;0)

.

(-2;3)

.

Câu 4 (1đ):

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

2x\le 5y+3z

.

2x<3y-5

.

2x^2+5y>3

.

3x^2+2x-4>0

.

Câu 5 (1đ):

Hình biểu diễn của tập hợp $A=\big\{ x \in \mathbb{R} \, \big| \, 1 \le x<3 \big\}$ (phần không bị gạch) trên trục số là

Câu 6 (1đ):

Cho tập hợp $B$ gồm các số nguyên tố có một chữ số. Tập hợp $B$ viết bằng cách liệt kê các phần tử của tập hợp là

B=\left\{ 1;2;3;5;7 \right\}

.

B=\left\{ 4;6;8;9 \right\}

.

B=\left\{ 2;3;5;7 \right\}

.

B=\left\{ 3;5;7 \right\}

.

Câu 7 (1đ):

Mệnh đề

A

đúng thì mệnh đề phủ định

\overline{A}

sai. Ngược lại, mệnh đề

A

sai thì mệnh đề phủ định

\overline{A}

đúng.

Cho hai mệnh đề: $P$ : " $30$ không chia hết cho $5$ " và $Q$ : " $\pi < 3,15$ ". Khẳng định nào sau đây đúng?

\overline{P}

đúng,

\overline{Q}

sai.

\overline{P}

sai,

\overline{Q}

đúng.

\overline{P}

đúng,

\overline{Q}

đúng.

\overline{P}

sai,

\overline{Q}

sai.

Câu 8 (1đ):

Tam giác $ABC$ có $\widehat{A}=105^\circ$ , $\widehat{B}=45^\circ$ , $AC=10$ . Độ dài cạnh $AB$ bằng

5\sqrt{2}

.

10\sqrt{2}

.

\dfrac{5\sqrt{6}}{2}

.

5\sqrt{6}

.

Câu 9 (1đ):

Đẳng thức nào sau đây sai?

\sin 60^\circ +\cos 150^\circ = 0

.

\sin 45^\circ + \sin 45^\circ = \sqrt{2}

.

\sin 120^\circ +\cos 30^\circ = 0

.

\sin 30^\circ + \cos 60^\circ = 1

.

Câu 10 (1đ):

Trong tam giác $ABC$ có bán kính đường tròn ngoại tiếp $R$ , hệ thức nào sau đây sai?

\sin C=\dfrac{c.\sin A}{a}

.

b=R.\tan B

.

a=2R.\sin A

.

a=\dfrac{b.\sin A}{\sin B}

.

Câu 11 (1đ):

Cho biết $\cos \alpha =-\dfrac23.$ Giá trị của $P=\dfrac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$ bằng

-\dfrac{19}{13}.

\dfrac{25}{13}.

\dfrac{19}{13}.

-\dfrac{25}{13}.

Câu 12 (1đ):

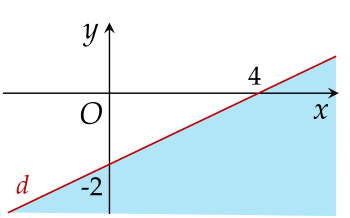
Phần tô màu (không bao gồm đường thẳng $d$ ) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?

loading...

2x-4y>-3

.

2x-4y>-5

.

x-2y<4

.

x-2y>4

.

Câu 13 (1đ):

Cho các hệ bất phương trình sau: $\left\{ \begin{aligned} &x-2y \le 0 \\&5x-y \ge -4 \\&x+2y \le 5 \\ \end{aligned} \right.$ , $\left\{ \begin{aligned} &-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned} &x-2y\le 0 \\ &5x-y\ge -4 \\ &x+2y\le 5 \\ \end{aligned} \right.$ là miền tam giác.
b) Điểm $M(1;1)$ thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&x-2y\le 0 \\&5x-y\ge -4 \\&x+2y\le 5 \\ \end{aligned} \right.$ .
c) Miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\&y\le 6 \\ \end{aligned} \right.$ là miền tứ giác.
d) Điểm $O(0;0)$ không thỏa mãn miền nghiệm của hệ bất phương trình $\left\{ \begin{aligned}&-x-y<4 \\&-x+2y>-2 \\&x+y<8 \\&x\ge -6 \\& y\le 6 \\ \end{aligned} \right.$ .

Câu 14 (1đ):

Cho ba tập hợp: $A=\left(-\infty ;1 \right]$ ; $B=\left[ -2;2 \right]$ và $C=\left(0;5 \right)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $C \subset A$ .
b) $A \cap C=\left(0;1 \right]$ .
c) $A \cap B=\left( -2;1 \right)$ .
d) $\left(A\cap B \right) \cup \left(A\cap C \right)=\left[ -2;1 \right]$ .

Câu 15 (1đ):

Cho $P(x)$ : " $x^2-x-2=0$ " với $x$ là các số thực.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $x=0$ thì $P(x)$ là mệnh đề đúng.
b) $P(-1)$ là mệnh đề sai.
c) $P(x)$ luôn là mệnh đề sai với $x$ là các số thực bất kì.
d) $P(2)$ là mệnh đề đúng.

Câu 16 (1đ):

Cho các tập hợp $C_{\mathbb{R}} A=\left[ -3;\sqrt{8} \right)$ , $C_{\mathbb{R}}B=\left(-5;2 \right) \cup \left(\sqrt{3};\sqrt{11} \right).$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $A=\left(-\infty ;\,-3 \right)\cup \left[ \sqrt{8};+\infty \right)$ .
b) $B=\left(-\infty ;-5 \right) \cup \left(\sqrt{11};+\infty \right)$ .
c) $A \cap B=\left(-\infty ;-5 \right) \cup \left[ \sqrt{8};+\infty \right)$ .
d) $C_{\mathbb{R} }\left(A\cap B \right)=\left(-5;\sqrt{11} \right)$ .

Câu 17 (1đ):

Trong đợt quyên góp ủng hộ đồng bào miền Bắc bị lũ lụt năm 2024, có $25$ học sinh lớp 2A đã tham gia ủng hộ, mỗi học sinh ủng hộ nhiều nhất hai tờ tiền khác nhau trong ba loại tờ tiền mệnh giá $5$ $000$ đồng, $10$ $000$ đồng và $20$ $000$ đồng. Biết rằng số học sinh đã tham gia ủng hộ thỏa mãn đồng thời ba kết quả sau:

(1) Số học sinh chỉ ủng hộ một tờ $5$ $000$ đồng bằng tổng số học sinh chỉ ủng hộ một tờ $10$ $000$ đồng và số học sinh chỉ ủng hộ một tờ $20$ $000$ đồng.

(2) Trong số học sinh không ủng hộ tờ $5$ $000$ đồng thì số học sinh có ủng hộ tờ $10$ $000$ đồng nhiều gấp hai lần số học sinh có ủng hộ tờ $20$ $000$ đồng.

(3) Số học sinh chỉ ủng hộ một tờ $5$ $000$ đồng nhiều hơn số học sinh ủng hộ tờ $5$ $000$ đồng và một tờ khác là $1$ học sinh.

Có bao nhiêu học sinh lớp 2A chỉ ủng hộ một tờ $10$ $000$ đồng?

Trả lời:

Câu 18 (1đ):

Cho hai tập hợp khác rỗng $A=\left(m-3;5 \right]$ , $B=\left(-2;\,3m+1 \right)$ với $m\in \mathbb{R}$ . Tìm số nguyên $m$ lớn nhất để $A\subset B$ .

Trả lời:

Câu 19 (1đ):

Để chuẩn bị cho đại hội chi đoàn 10A1, bạn Nga được phân công đi mua hoa để cắm vào $3$ lọ, mỗi lọ cắm số hoa mỗi loại như nhau. Bạn Nga được lớp giao cho $200$ nghìn đồng để mua nhưng đến quầy bán chỉ còn $2$ loại hoa và đã mua đủ để cắm. Biết rằng một loại hoa có giá $15$ nghìn đồng/bông và một loại có giá $20$ nghìn/bông. Số tiền dư ra ít nhất có thể là bao nhiêu nghìn đồng?

Trả lời:

Câu 20 (1đ):

Tìm giá trị nhỏ nhất của biểu thức $F=y-x$ trên miền xác định bởi hệ $\left\{ \begin{aligned}&y-2x \le 2 \\&2y-x \ge 4 \\ &x+y \le 5 \\ \end{aligned} \right.$ .

Trả lời:

Câu 21 (1đ):

Theo nghiên cứu, mỗi kilôgam thịt bò chứa $800$ đơn vị protein và 200 đơn vị lipit., mỗi kilôgam thịt lợn chứa $600$ đơn vị protein và $400$ đơn vị lipit. Một gia đình cần ít nhất $900$ đơn vị protein và $400$ đơn vị lipit trong thức ăn mỗi ngày. Biết rằng gia đình này chỉ mua nhiều nhất $1,6$ kg thịt bò và $1,1$ kg thịt lợn. Giá tiền một kg thịt bò là $160$ nghìn đồng, một kg thịt lợn là $110$ nghìn đồng. Gọi $x, \, y$ lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính $x^2 + y^2$ (làm tròn đến chữ số thập phân thứ nhất).

Trả lời:

Câu 22 (1đ):

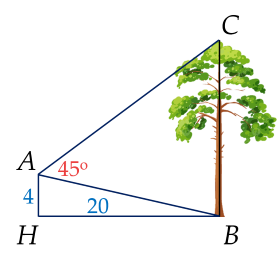
loading...

Từ vị trí $A$ người ta quan sát một cây cao. Biết $AH=4$ m, $HB=20$ m, $\widehat{BAC}=45^\circ$ . Tính chiều cao của cây (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị mét)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP