Bài học cùng chủ đề
- Phương trình và hệ phương trình bậc nhất ba ẩn
- Giải hệ phương trình bậc nhất ba ẩn dạng tam giác
- Giải hệ phương trình bậc nhất ba ẩn bằng phương pháp Gauss
- Số nghiệm của hệ phương trình bậc nhất ba ẩn
- Giải hệ phương trình bậc nhất ba ẩn bằng máy tính cầm tay
- Phương trình và hệ phương trình bậc nhất ba ẩn
- Bài toán thực tế ứng dụng hệ phương trình bậc nhất ba ẩn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Số nghiệm của hệ phương trình bậc nhất ba ẩn SVIP

Nếu video không chạy trên Zalo, bạn vui lòng Click vào đây để xem hướng dẫn
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Theo dõi OLM miễn phí trên Youtube và Facebook:
Đây là bản xem trước câu hỏi trong video.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
Câu 1 (1đ):
Cho hệ phương trình ⎩⎨⎧x+y+z=32x+y−z=55x+4y+2z=7
Để khử đi ẩn x ở phương trình thứ hai, ta nhân phương trình thứ nhất với rồi cộng với phương trình thứ hai theo từng vế tương ứng.
Câu 2 (1đ):
Cho hệ phương trình ⎩⎨⎧x+y+z=32x+y−z=55x+4y+2z=7
Để khử đi ẩn x ở phương trình thứ ba, ta nhân phương trình thứ nhất với rồi cộng với phương trình thứ ba theo từng vế tương ứng.
Câu 3 (1đ):
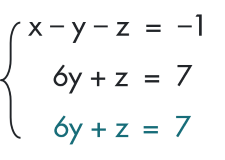
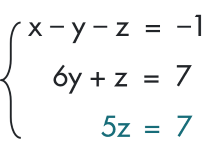
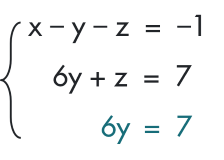
Từ hệ phương trình 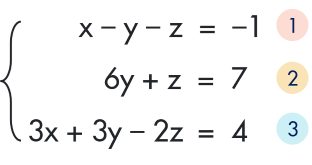
Nhân hai vế của  với (–3) rồi cộng với
với (–3) rồi cộng với  ta được hệ phương trình mới là
ta được hệ phương trình mới là
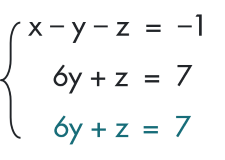
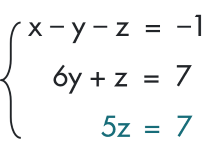
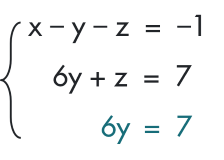
Câu 4 (1đ):
Chọn tất cả các phương án đúng:
Một hệ phương trình bậc nhất ba ẩn có thể có
vô nghiệm.
đúng ba nghiệm.
vô số nghiệm.
nghiệm duy nhất.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- [âm nhạc]
- ở đây chúng ta sẽ nhân
- chính sách Nhân hai vế của phương trình
- 1 với âm 2 rồi cộng với phương trình 2
- theo từng vế tướng ta sẽ thu được phương
- trình thứ nhất và phương trình cuối cùng
- giữ nguyên phương trình 1 khi nhân với
- âm 2 ta được trừ 2X - 2y - 2z = -6 nhớ
- là nhân cả hai vế nhá phương trình 2 ta
- giữ nguyên thì khi cộng lại trừ 2X + 2x
- sẽ bằng 0 này - 2y + Y sẽ bằng - y - 2z
- cộng với trừ Z là -3z như vậy trừ y trừ
- 3Z còn vế phải -6 + 5 = -1 ta thu được
- hệ phương trình mới như thế này
- bước tiếp theo các bạn tiếp tục khử đi
- 5x ở phương trình cuối cùng
- rất chính xác để khử đi 5x ta Nhân hai
- vế của phương trình 1 với âm 5 rồi cộng
- với cái chương trình 3 theo từng vế
- tương ứng thì phương trình thứ nhất và
- phương trình thứ hai này hai phương
- trình này nhé chúng ta giữ nguyên phương
- trình 1 khi nhân với âm 5 ta được trừ 5x
- - 5y - 5z = -15 phương trình 3 giữ
- nguyên thì khi cộng các vế tương ứng lại
- trừ 5x + 5x = 0 trừ 5y + 4 y = - y - 5z
- + 2z = -3z Như vậy vẫn là trừ y trừ 3 z
- ở vế trái
- vế phải âm 15 + 7 ta được âm 8 và ta có
- hệ phương trình trở thành như thế này
- như vậy sau 2 bước Thì ta đưa được về hệ
- phương trình mà có phương trình thứ hai
- và phương trình thứ ba thầy làm nổi bật
- bằng màu xanh sẽ có một đặc điểm khá đặc
- biệt đó là vế trái của chúng giống hệt
- nhau dẫn tới vế phải là âm 1 và 8 cũng
- phải bằng nhau thôi nhưng âm 1 bằng 8
- thì là vô lý Cho nên hệ phương trình này
- của chúng ta vô nghiệm dẫn tới hệ phương
- trình ban đầu là một hệ phủ nghiệm và
- bên cạnh việc trình bày theo từng bước
- này nếu các bạn đã làm thuần thục thì
- các bước này chúng ta có thể làm ra nháp
- và trình bày trong bài Ta sẽ viết các
- phép biến đổi tương đương như thế này
- nhưng vẫn phải đảm bảo theo từng bước
- làm phía trên sau khi tới đây do âm 1
- bằng 8 là vô lý nên ta kết luận hệ
- phương trình đã cho vô nghiệm khi ta
- viết như thế này là ta đang biến đổi
- tương đương và các bạn nhớ trong phép
- biến đổi tương đương phần phía trước và
- phần phía sau phải có tập nghiệm giống
- nhau thì chúng ta mới được viết tương
- đương nhé Cho nên để đảm bảo nghiệm
- không thay đổi thì chúng ta phải tuân
- thủ đúng các bước biến đổi theo phương
- pháp gau mà đã học ở phần trước
- vậy Liệu hệ phương trình chỉ dừng lại ở
- hai trường hợp vô nghiệm và có nghiệm
- duy nhất hay không Chúng ta sẽ đến với
- câu hỏi hỏi chấm 9 Thầy yêu cầu giải hệ
- phương trình này
- chúng ta vẫn thực hiện bước đầu tiên là
- nhiều chỗ phương trình thứ nhất cho
- phương trình thứ hai bởi vì thấy thấy hệ
- số x = 1 ở đây ở phương trình thứ hai ta
- thu được hệ phương trình như thế này và
- bắt đầu các vách biến đổi như sau thầy
- ký hiệu phương trình 1 2 3 để chúng ta
- dễ gọi tên trước tiên là khử đi ẩn x ở
- phương trình thứ hai ta nhân phương
- trình thứ nhất với âm 5 rồi cộng với
- phương trình thứ hai theo từng với tương
- ứng ta sẽ thu được phương trình thứ nhất
- và phương trình thứ ba giữ nguyên trước
- khi cộng với phương trình 2 thì phương
- trình thứ nhất nhân với -5 ta được trừ
- 5x + 5y + 5z = 5 cộng các vị tương ứng
- phần này bằng 0 này 5y + y = 6y
- 5z + -4z = z như vậy 6y + z = 5 + 2 = 7
- ta được hệ phương trình mới như thế này
- tiếp theo các bạn tiếp tục khử đi ẩn x ở
- phương trình thứ hai cho thầy nhé
- chính xác rồi ta nhân hai tâm lý của
- phương trình 1 với âm 3 rồi cộng với
- phương trình thứ 3 theo từng vế ta sẽ
- thu được 3 y + 3y là 6y
- 3Z + -2z là Z và 3 + 4 = 7 như vậy qua
- hai phép biến đổi đầu tiên thì hệ phương
- trình của chúng ta đã trở thành hệ
- phương trình này thành biểu diễn bằng
- các phép biến đổi tương đương có một đặc
- điểm đặc biệt ở hai phương trình thầy
- làm nổi bật bằng màu đỏ là chúng giống
- hệt nhau khi đó hệ phương trình của
- chúng ta còn được viết thành x trừ y trừ
- z bằng -1 và 6y + Z = 7 một hệ phương
- trình ba ẩn nhưng chỉ gồm có hai phương
- trình thôi phương trình thứ nhất của 3
- ẩn phương trình thứ hai gồm hai ẩn ta
- gọi đó là một hệ phương trình của dạng
- hình thang và nếu các bạn gặp hệ phương
- trình dạng như thế này ta sẽ kết luận đó
- là một hệ phương trình có vô số nghiệm
- nhé Còn để rõ ràng hơn thầy sẽ tiếp sử
- dụng biến đổi bằng cách
- 6y + Z = 7 giữ nguyên Z ở vế trái chuyển
- tất cả sang vế phải ta thu được Z = 7 -
- 6y sau đó thay lên phương trình phía
- trên chỗ nào có Z ta thay bằng 7 - 6y ta
- sẽ thu được x = -5y + 6 như vậy Ở đây ta
- đã biểu diễn được X và Z theo y còn y
- thì không có điều kiện ràng buộc nào cho
- nên y là một số thực bất kỳ thì X và Z
- cũng sẽ nhận các giá trị tương ứng do đó
- hệ phương trình của chúng ta sẽ có vô số
- nghiệm và tập nghiệm của hệ thầy ký hiệu
- là s sẽ bằng -5y + 6 chỉ là x này
- y và 7 - 6y tất cả ta đều đưa được về
- theo Ẩn Y Y là một số thực bất kỳ và đó
- là kết luận về nghiệm của hệ phương
- trình ở hỏi chấm 9 như vậy qua các ví dụ
- vừa rồi thì các bạn có thể thấy một hệ
- phương trình của chúng ta sẽ có 3 trường
- hợp có thể có một nghiệm vô số nghiệm
- hoặc là vô nghiệm tương ứng với các ví
- dụ hệ phương trình thứ nhất là vô nghiệm
- hệ phương trình thứ hai là vô số nghiệm
- và hệ phương trình cuối cùng là có một
- nghiệm duy nhất đó cũng là kết luận về
- số nghiệm của hệ phương trình bậc nhất
- ba ở trong phần cuối cùng bên cạnh việc
- biến đổi về các phương trình đơn giản
- hơn thì chúng ta còn có thể sử dụng máy
- tính cầm tay để giải hệ phương trình bậc
- nhất ba ẩn nhé
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
