Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Số hữu tỉ. Biểu diễn số hữu tỉ trên trục số SVIP
Tải đề xuống bằng file Word
I. SỐ HỮU TỈ
Số hữu tỉ là số viết được dưới dạng phân số \(\dfrac{a}{b}\) với \(a,b\inℤ,b\ne0\).
Tập hợp các số hữu tỉ được kí hiệu là \(ℚ\).
Ví dụ: Các số: \(-9\); \(0\); \(-6,5\); \(1\dfrac{1}{3}\) có là số hữu tỉ không? Vì sao?
Giải
Các số đã cho là số hữu tỉ vì mỗi số đó đều viết được dưới dạng phân số. Cụ thể là:
\(-9=\dfrac{-9}{1}\); \(0=\dfrac{0}{1}\); \(-6,5=\dfrac{-65}{10}\); \(1\dfrac{1}{3}=\dfrac{4}{3}\).
Chú ý:
- Mỗi số nguyên là một số hữu tỉ.
- Các phân số bằng nhau là các cách viết khác nhau của cùng một số hữu tỉ.
Ví dụ: Vì \(\dfrac{1}{3}=\dfrac{2}{6}\) nên hai phân số \(\dfrac{1}{3}\) và \(\dfrac{2}{6}\) cùng biểu diễn một số hữu tỉ.
II. BIỂU DIỄN SỐ HỮU TỈ TRÊN TRỤC SỐ
Trên trục số, điểm biểu diễn số hữu tỉ \(a\) được gọi là điểm \(a\).
Do các phân số bằng nhau cùng biểu diễn một số hữu tỉ nên khi biểu diễn số hữu tỉ trên trục số, ta có thể chọn một trong những phân số đó để biểu diễn số hữu tỉ trên trục số. Thông thường, ta chọn phân số tối giản để biểu diễn số hữu tỉ đó.
Ví dụ: Biểu diễn số hữu tỉ \(\dfrac{2}{5}\) trên trục số.
Để biểu diễn số hữu tỉ \(\dfrac{2}{5}\) trên trục số, ta làm như sau:
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 5 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{5}\) đơn vị cũ);
- Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 2 đơn vị mới đến điểm \(A\). Điểm \(A\)biểu diễn số hữu tỉ \(\dfrac{2}{5}\).
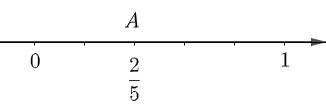
Hình 1
Nhận xét: Do \(\dfrac{4}{10}=\dfrac{2}{5}\). Nên điểm A ở Hình 1 cũng là điểm biểu diễn số hữu tỉ \(\dfrac{4}{10}\) trên trục số.
Ví dụ: Biểu diễn số hữu tỉ \(\dfrac{-1}{3}\) trên trục số.
Để biểu diễn số hữu tỉ \(\dfrac{-1}{3}\) trên trục số, ta làm như sau:
- Chia đoạn thẳng đơn vị (chẳng hạn từ điểm 0 đến điểm 1) thành ba phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ);
- Đi theo chiều ngược với chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 1 đơn vị mới đến điểm B. Điểm B biểu diễn số hữu tỉ \(\dfrac{-1}{3}\).
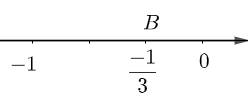
Hình 2
Ví dụ: Biểu diễn số hữu tỉ \(1,5\) trên trục số, ta làm như sau:
- Viết \(1,5\) về dạng phân số tối giản \(1,5=\dfrac{3}{2}\);
- Chia đoạn thẳng đơn vị (chẳng hạn từ điểm 0 đến điểm 1) thành 2 phần bằng nhau, lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\dfrac{1}{2}\) đơn vị cũ);
- Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy 3 đơn vị mới đến điểm C. Điểm C biểu diễn số hữu tỉ 1,5.
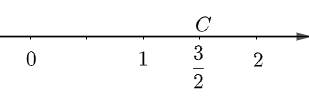
Hình 3
Bạn có thể đăng câu hỏi về bài học này ở đây
