Bài học cùng chủ đề
- Quy tắc cộng, quy tắc nhân và sơ đồ hình cây
- Quy tắc cộng
- Quy tắc nhân
- Kết hợp quy tắc cộng và quy tắc nhân
- Các bài toán đếm thường gặp: đếm số (cơ bản)
- Các bài toán đếm thường gặp: chọn người chọn vật + hình học (cơ bản)
- Quy tắc cộng
- Quy tắc nhân
- Đếm bằng sơ đồ hình cây
- Bài toán kết hợp quy tắc cộng và quy tắc nhân
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Quy tắc cộng, quy tắc nhân và sơ đồ hình cây SVIP
I. QUY TẮC CỘNG
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có \(m\) cách thực hiện, hành động thứ hai có \(n\) cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc có \(m+n\) cách hoàn thành.
Nhận xét:
Ta có quy tắc sau: Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có \(m\) cách thực hiện, hành động thứ hai có \(n\) cách thực hiện, hành động thứ ba có \(p\) cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì công việc có \(m+n+p\) cách hoàn thành.
Ví dụ. Lớp \(10\)A có \(40\) học sinh, lớp \(10\)B có \(38\) học sinh. Có bao nhiêu cách cử một học sinh của lớp \(10\)A hoặc của lớp \(10\)B tham gia buổi giao lưu các học sinh trong các trường trung học phổ thông trong tỉnh sắp diễn ra?
Giải
Công việc cử một học sinh có hai phương án lựa chọn:
Phương án một: cử một học sinh của lớp \(10\)A có \(40\) cách thực hiện.
Phương án hai: cử một học sinh của lớp \(10\)B có \(38\) cách thực hiện.
Theo quy tắc cộng có \(40+38=78\) cách chọn một học sinh tham gia buổi giao lưu các học sinh trong các trường trung học phổ thông trong tỉnh.
II. QUY TẮC NHÂN
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có \(m\) cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có \(n\) cách hành động thứ hai thì công việc đó có \(m.n\) cách hoàn thành.
Nhận xét:
Ta có quy tắc sau: Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có \(m\) cách thực hiện; ứng với mỗi cách thực hiện hành động thứ nhất, có \(n\) cách hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có \(p\) cách thực hiện hành động thứ ba thì công việc đó có \(m.n.p\) cách hoàn thành.
Ví dụ. Lan có \(5\) chiếc áo và \(3\) chiếc quần. Lan có bao nhiêu cách lựa chọn một bộ quần áo để mặc đi chơi.
Giải
Việc chọn một bộ quần áo của Lan có thể coi như là hai công đoạn:
Công đoạn \(1\): chọn một chiếc áo từ \(5\) chiếc áo, có \(5\) cách thực hiện công đoạn này.
Công đoạn \(2\): chọn một chiếc quần từ \(3\) chiếc quần, có \(3\) cách thực hiện công đoạn này.
Áp dụng quy tắc nhân, có \(5.3=15\) cách lựa chọn một bộ quần áo để mặc đi chơi.
III. SƠ ĐỒ HÌNH CÂY
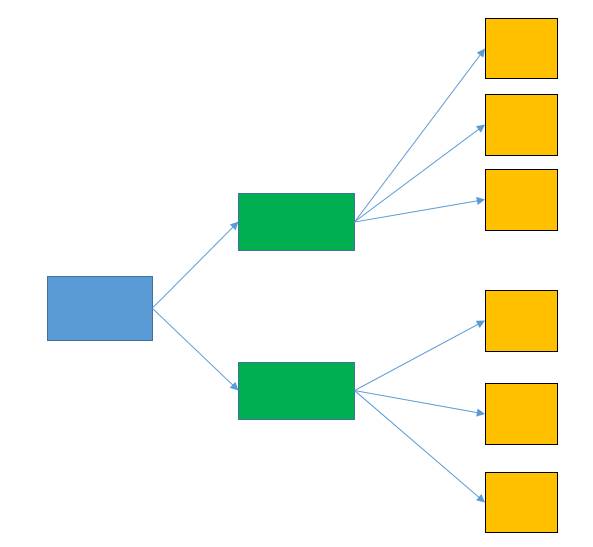
Nhận xét:
- Sơ đồ hình cây ở trên là sơ đồ bắt đầu tại một nút duy nhất với các nhánh tỏa ra các nút bổ sung.
- Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.
IV. VẬN DỤNG TRONG BÀI TOÁN ĐẾM
1. Vận dụng trong giải toán
Ví dụ. Từ các số \(0,1,2,3,4\) có thể lập được bao nhiêu:
a) số tự nhiên có \(4\) chữ số khác nhau?
b) số tự nhiên chẵn có \(4\) chữ số khác nhau?
Giải
Gọi số cần lập là \(\overline{abcd}\) với \(a,b,c,d\) là bốn chữ số khác nhau từ các chữ số đã cho.
a) Có \(4\) cách chọn chữ số \(a\) từ \(4\) chữ số khác \(0\) đã cho.
Với mỗi cách chọn \(a\), có \(4\) cách chọn chữ số \(b\) từ \(4\) chữ số còn lại.
Ứng với mỗi cách chọn \(b\) đó, có \(3\) cách chọn chữ số \(c\) từ \(3\) chữ số còn lại.
Ứng với mỗi cách chọn \(c\) đó, có \(2\) cách chọn chữ số \(d\) từ \(2\) chữ số còn lại.
Áp dụng quy tắc nhân có: \(4.4.3.2=96\) số tự nhiên có \(4\) chữ số khác nhau được lập từ các số đã cho.
b) Để \(\overline{abcd}\) là số chẵn, chữ số \(d\) phải là chữ số chẵn. Vậy có hai trường hợp:
Trường hợp \(1:\)\(d=0\) khi đó có \(4\) cách chọn chữ số \(a\) từ \(4\) chữ số còn lại, ứng với mỗi cách chọn \(a\) đó có \(3\) cách chọn chữ số \(b\) từ \(3\) chữ số còn lại. Với mỗi cách chọn \(b\), có \(2\) cách chọn chữ số \(c\) từ \(2\) chữ số còn lại.
Áp dụng quy tắc nhân có: \(4.3.2=24\) số thỏa mãn.
Trường hợp \(2:\)\(d=2\) hoặc \(d=4\).
Khi đó có \(2\) cách chọn chữ số \(d\) từ \(2\) chữ số \(2\) hoặc \(4\). Với mỗi cách chọn đó có \(3\) cách chọn chữ số \(a\) từ \(3\) chữ số khác \(0\) còn lại. Với mỗi cách chọn \(a\), có \(3\) cách chọn chữ số \(b\) từ \(3\) chữ số còn lại, Với mỗi cách chọn \(b\), có \(2\) cách chọn chữ số \(c\) từ \(2\) chữ số còn lại.
Áp dụng quy tắc nhân có: \(2.3.3.2=36\) số thỏa mãn.
Theo quy tắc cộng có: \(24+36=60\) số chẵn có \(4\) chữ số khác nhau thỏa mãn.
2. Vận dụng trong thực tiễn
Ví dụ: Cho kiểu gen AaBbDd. Biết quá trình giảm phân tạo giao tử bình thường, không xảy ra đột biến
a) Vẽ sơ đồ hình cây biểu thị sự hình thành giao tử.
b) Từ đó, tính số loại giao tử của kiểu gen AaBbDd.
Giải
a) Sơ đồ hình cây biểu thị sự hình thành giao tử:
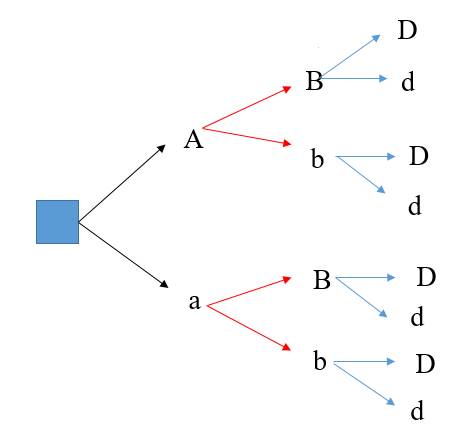
b) Từ sơ đồ hình cây, ta có \(8\) loại giao tử của kiểu gen AaBbDd.
Bạn có thể đăng câu hỏi về bài học này ở đây
