Bài học cùng chủ đề
- Giá trị lượng giác của một góc từ 0 độ đến 180 độ
- Giá trị lượng giác của một góc từ 0° đến 180°
- Quan hệ giữa các giá trị lượng giác của 2 góc bù nhau
- Định lí côsin
- Định lí sin
- Tính giá trị lượng giác của một góc bất kì từ 0° đến 180°
- Quan hệ của GTLG của hai góc bù nhau, phụ nhau
- So sánh các GTLG. Tính giá trị biểu thức lượng giác
- Luyện tập tổng hợp và GTLG một góc từ 0° đến 180°
- Định lí côsin, định lí sin và ứng dụng
- Bài tập tự luận (nâng cao)
- Phiếu bài tập: Giá trị lượng giác của một góc
- Phiếu bài tập: Định lí sin - côsin
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Quan hệ giữa các giá trị lượng giác của 2 góc bù nhau SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Quan hệ giữa các giá trị lượng giác của 2 góc bù nhau
Đối với hai góc bù nhau, $\alpha$ và $180^{\circ}-\alpha$, ta có:
- $\sin \left(180^{\circ}-\alpha\right)=\sin \alpha$.
- $\cos \left(180^{\circ}-\alpha\right)=-\cos \alpha$;
- $\tan \left(180^{\circ}-\alpha\right)=-\tan \alpha\left(\alpha \neq 90^{\circ}\right)$
- $\cot \left(180^{\circ}-\alpha\right)=-\cot \alpha\left(0^{\circ}<\alpha<180^{\circ}\right)$.
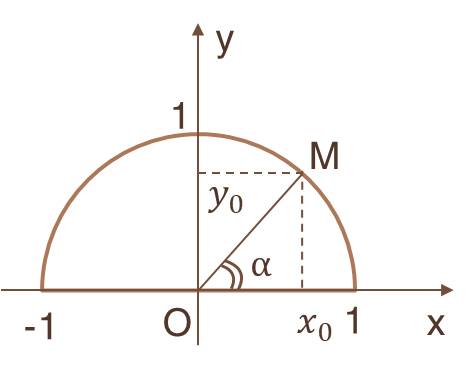
Trong hình trên, có xOM=α, điểm N thỏa mãn xON=180∘−α nằm đối xứng với M qua .
(Kéo thả hoặc click vào để điền)
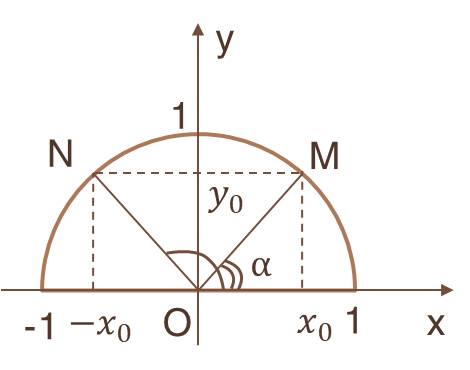
Trong hình trên, xOM=α,xON=180∘−α.
⚡ cosα=x0;
⚡ cos(180∘−α)= .
(Kéo thả hoặc click vào để điền)
Hoàn thành nhận xét sau.
Hai góc bù nhau có sin
- đối nhau
- bằng nhau
- đối nhau
- bằng nhau
Điền số đo của một góc nhọn thích hợp.
sin120∘=sin o.
Điền số thích hợp vào ô trống.
sin150∘= ;
cos150∘= ;
tan150∘= ;
cot150∘= .
(Kéo thả hoặc click vào để điền)
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- ở
- bên rồi ta sẽ tìm hiểu về mối quan hệ
- của các giá trị lượng giác của hai góc
- bù nhau
- phải có Alpha thì góc bù với nó sẽ có số
- đo là
- 180 độ - Alpha cái gì đây thì đã dựng ra
- hai góc bù nhau ở trên để cho đơn vị em
- chú ý là để dự các góc trên đường tròn
- đơn vị chúng ta luôn lấy một một cạnh
- góc là Ox á thì thấy dựng góc x om
- góc xom bằng
- và con số đó là anh ta bây giờ thấy muốn
- dựng một góc bù với Alpha Tức là nó có
- số đo là 180 độ
- 3 - đèn pha thì thay cần tìm điểm n trên
- đường cho đơn vị sao cho là góc x ol
- khi con số là 189 ta thì khi đó chúng ta
- mới nhận xét được các giá trị lượng giác
- của góc Alpha và góc bù với con pha kem
- phải chú ý nhá Tìm giao điểm N có khói
- không ra là đơn giản thấy có là góc x o
- o o bằng Alpha rồi ta chỉ cần lấy đối
- xứng với M qua trục tung thì ta sẽ có
- điểm lên nữa bởi vì sao góc ít onl này
- lại bù với góc bởi vì chúng ta sẽ có là
- góp
- anh tóc này
- Ừ nó cũng bật đèn pha cho nên là góc x
- sẽ bằng 180° chưa Pha chứng minh cái này
- thì rất là được làm chúng ta vận dụng
- những kiến thức về góc cơ bản đã học ở
- lớp 7 rồi Vậy thì điểm N và để mở nó đối
- xứng với nhau qua trục
- công việc của chúng ta bây giờ là Xem
- mối liên hệ của các giá trị lượng giác
- của góc Alpha và 180 độ chuyển pha như
- thế nào
- anh ở đây thì phải đã biết sẵn ra là gì
- sinh Alpha và sin 100 độ đèn pha tương
- tự cushion tang cotang thí nghiệm vụ
- Chúng ta là gì ta sẽ điền xem là trước
- của Shin cu Shin tacota 189 xanh này nó
- là dấu cộng chưa Nếu dấu cộng với tài
- nguyên giống - đã đến đấu trường vào xin
- Alpha tức là tung lượng để mở
- ở tốc độ điểm m lạ Y không Con xin 180
- độ trường pha nó là
- có tung độ để n Ta thấy nó cũng nghỉ
- không như vậy xin Alpha sẽ bằng xin cho
- thằng đội Trường Sa
- anh xin hai góc bù nhau thì bằng nhau à
- anh với koshi thì sao
- số cosin của pha tức lá hoàng động để mờ
- lại không
- Anh kosen của 180 chuyển pha nó là Hoàng
- Động điện n Thì thấy nó là a đối với
- Không là chửi không như vậy thì ta cần
- nhìn đâu trừ đây
- Anh kosen của hai góc bù nhau thì đối
- nhau
- trực tiếp từ nhận xét được sim vào code
- gì tao thì dễ làm thì sẽ được tang và
- côtang A
- Ê tao thấy
- em xin thì bằng nhau cô xin đổi nhau như
- vậy tanh sẽ đối nhau và cô ta cũng đưa
- nhau như vậy thì nhớ một cách đơn giản
- là hai góc bù nhau thì xin bằng nhau
- caution đối nhau tang đối nhau và cô ta
- đánh nhau chỉ cần nhớ xin bằng nhau và
- cô xin lỗi nhau ta có thể suy ra tang và
- cổ tay của đội nhau rồi Đây là mối liên
- hệ rất là cơ bản thì các em cần phải ghi
- nhớ chúng ta không thể quên cũng như
- không được nhầm về ca sĩ chắc này
- ạ bây giờ áp dụng mối quan hệ vừa rồi
- Chúng ta sẽ tìm các giá trị lượng giác
- của một vài các đặc biệt cụ thể ở đây là
- góc 120 độ và các 150 độ góc 135 độ thì
- ta đã làm ở bài trước rồi người ta sẽ
- tìm hiểu về góc 120 độ và chân ấy độ
- cũng là các cấp rất hay gặp bây giờ thì
- sẽ làm với 120 trước sau đó lại các em
- sẽ làm với 150 độ nhé với góc 120 độ thì
- đầu tiên thấy Tìm xin của 120 độ
- em xin 120 độ tại áp dụng vào đây ta sẽ
- đưa về giá trị lượng giác của góc nhọn
- em mới góc nhọn thì chúng ta cũng đã
- biết được giá trị lượng giác của một số
- rác đặc biệt Thế thì xin trong 20 đội ta
- sẽ đưa về góc đặc biệt nào góc nhọn đặc
- biệt nào áp dụng gì hết này Sin của góc
- bù nhau đều nhau thì sẽ đưa về xin của
- 180 độ - - 120 độ
- em và nó bằng
- em xin của 60 độ sinh 60 độ thì ta biết
- nó là bao nhiêu
- sin30 bằng 1/2 sin60 = căn 3 trên 2
- cosin của 120 độ
- Ừ để đưa về ta sẽ đưa về cosin của của
- 60 độ là góc bù với trường với độ thế
- thì áp dụng
- về mối quan hệ của cu Shin cu Shin hay
- các hộ nghèo thì đối nhau tại thành -
- có được kết quả là -1 phần 2
- anh vàng cũng vậy tanh một 20 độ thì
- bằng đối của tao
- a 60 độ
- 360 độ ta đã biết nó bằng thanh bằng căn
- 3 Nếu không Nhớ thì ta có thể lấy cái
- mai thứ hai triệu một tháng hay là căn 3
- như vậy trừ của tao 60 độ là chỉ cần 3
- Và cô ta 120 độ
- nó sẽ là nghịch đảo của tang Tức là nó
- bằng - 1983 tương tự như vậy với các 150
- độ thì cái máy cho thấy cái quạt cái gì
- đáng giá của nó cũng thông qua cách sử
- dụng mối quan hệ này à
Bạn có thể đăng câu hỏi về bài học này ở đây
