Bài học cùng chủ đề
- Một số dấu hiệu nhận biết tứ giác nội tiếp
- Chứng minh tứ giác nội tiếp (Phần 1)
- Chứng minh tứ giác nội tiếp (Phần 2)
- Tứ giác nội tiếp
- Tứ giác nội tiếp
- Phương pháp: Chứng minh tổng hai góc đối bằng 180 độ
- Phương pháp: Chứng minh hai đỉnh kề nhau cùng nhìn cạnh chứa hai điểm còn lại hai góc bằng nhau
- Phương pháp: Chứng minh góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện
- Chứng minh đẳng thức tích các đoạn thẳng
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phương pháp: Chứng minh tổng hai góc đối bằng 180 độ SVIP
Cho nửa đường tròn tâm $O$ đường kính $AB = 2R$, $D$ là một điểm tùy ý trên nửa đường tròn ($D$ khác $A$ và $B$). Các tiếp tuyến với nửa đường tròn $(O)$ tại $A$ và $D$ cắt nhau tại $C$.
Chứng minh $OACD$ là tứ giác nội tiếp.
Hướng dẫn giải:
Do $AC$, $DC$ là các tiếp tuyến của đường tròn $(O)$ nên \(\widehat{CAO}=\widehat{CDO}=90^o\)
Xét tứ giác $OACD$ có \(\widehat{CAO}+\widehat{CDO}=180^o\) nên OACD là tứ giác nội tiếp.
a) Chứng minh rằng tứ giác $APMQ$ nội tiếp một đường tròn.
Hướng dẫn giải:
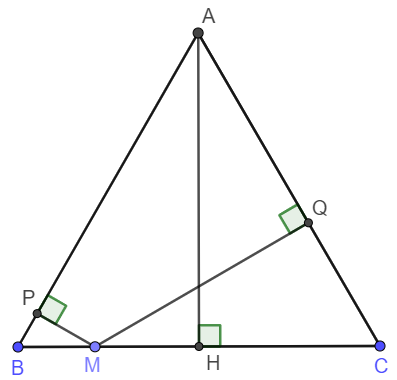
Xét tứ giác APMQ có \(\widehat{APM}+\widehat{AQM}=90^o+90^o=180^o\)
Nên tứ giác APMQ là tứ giác nội tiếp (Dấu hiệu nhận biết).
Cho đường tròn tâm $O$ đường kính $AB = 2R$. Gọi $C$ là trung điểm của $OA$; qua $C$ kẻ đường thẳng vuông góc với $OA$ cắt đường tròn đó tại hai điểm phân biệt $M$ và $N$. Trên cung nhỏ $BM$ lấy điểm $K$ ($K$ khác $B$ và $M$). Gọi $H$ là giao điểm của $AK$ và $MN$. Chứng minh rằng tứ giác $BCHK$ là tứ giác nội tiếp.
Hướng dẫn giải:
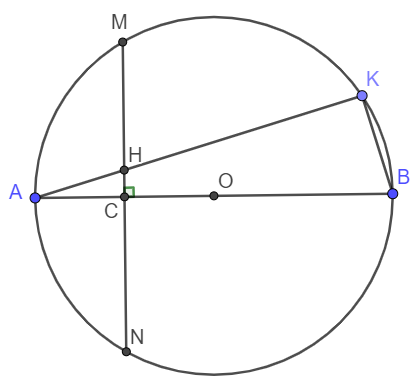
Do K thuộc đường tròn nên \(\widehat{HKB}=90^o\). Do CH vuông góc với AB nên \(\widehat{HCB}=90^o\)
Xét tứ giác BCHK có \(\widehat{HKB}+\widehat{HCB}=180^o\) nên BCHK là tứ giác nội tiếp.
Cho tam giác $ABC$ có $3$ góc nhọn. Đường tròn $(O;R)$ đường kính $BC$ cắt $AB$, $AC$ lần lượt tại $F$ và $E$; $BE$ cắt $CF$ tại $H$. $AH$ cắt $BC$ tại $D$.
a) Chứng minh tứ giác $AFHE$ nội tiếp. Xác định tâm $I$ của đường tròn ngoại tiếp tứ giác $AFHE$.
b) Chứng minh bốn điểm $D$, $E$, $I$, $F$ cùng nằm trên một đường tròn.
Hướng dẫn giải:
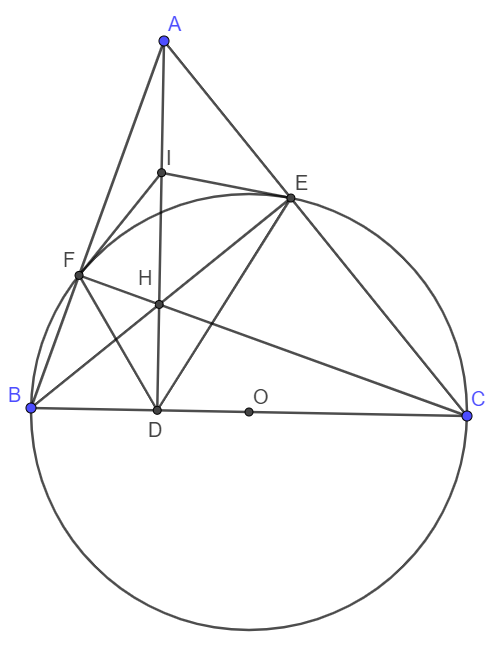
a) Vì E, F nằm trên đường tròn đường kính BC nên \(\widehat{BFC}=\widehat{BEC}=90^o\).
Suy ra tam giác AFH và AEH là hai tam giác vuông chung cạnh huyền AH, do đó F, E cùng nằm trên đường tròn đường kính AH. Vậy AFHE nội tiếp đường tròn tâm I với I là trung điểm AH.
b) Dễ thấy BFHD và CEHD là những tứ giác nội tiếp, vì vậy \(\widehat{FDH}=\widehat{FBH}=90^o-\widehat{BAC}\).
Tương tự \(\widehat{EDH}=90^o-\widehat{BAC}\Rightarrow\widehat{FDE}=180^o-2\widehat{BAC}\).
Mặt khác tứ giác AFHE nội tiếp nên \(2\widehat{BAC}=\widehat{FIE}\Rightarrow\widehat{FDE}=180^o-2\widehat{BAC}=180^o-\widehat{FIE}\).
Do đó \(\widehat{FDE}+\widehat{FIE}=180^o\) nên FIED là tứ giác nội tiếp.
Cho tứ giác $ABCD$ có $AC$ vuông góc với $BD$ tại $O$. Từ $O$ kẻ $OE$, $OF$, $OG$, $OH$ lần lượt vuông góc với các cạnh $AB$, $BC$, $CD$, $DA$. Chứng minh tứ giác $EFGH$ là tứ giác nội tiếp.
Hướng dẫn giải:
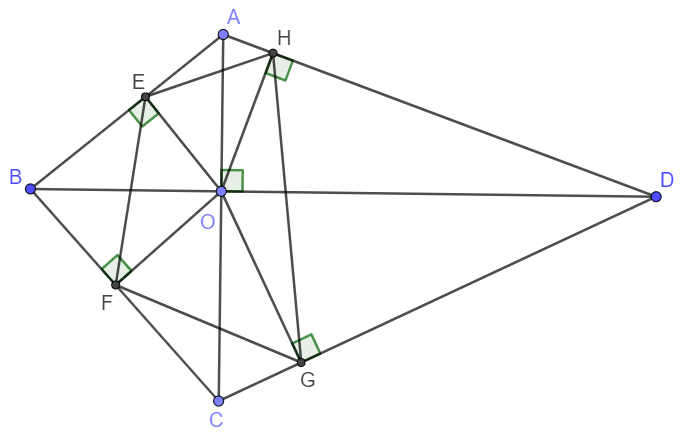
Ta chứng minh tổng góc hai góc đối của tứ giác EFGH bằng 180o.
Xét tứ giác BEOF có \(\widehat{BEO}+\widehat{BFO}=180^o\) nên BEOF là tứ giác nội tiếp.
Tương tự ta cũng có các tứ giác HOEA, OFCG, OGDH là các tứ giác nội tiếp.
Lại có AC vuông góc BC nên ta có: \(\widehat{FGH}+\widehat{FEH}=\left(\widehat{HGO}+\widehat{OGF}\right)+\left(\widehat{HEO}+\widehat{OEF}\right)\)\(=\left(\widehat{HDO}+\widehat{OCF}\right)+\left(\widehat{HAO}+\widehat{OBF}\right)\)
\(=\left(\widehat{OBF}+\widehat{OCF}\right)+\left(\widehat{HAO}+\widehat{HDO}\right)\)
\(=90^o+90^o=180^o\)
Vậy nên EFGH là tứ giác nội tiếp.
