Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phép nhân và phép chia số tự nhiên SVIP
1. PHÉP NHÂN SỐ TỰ NHIÊN
a. Nhân hai số tự nhiên
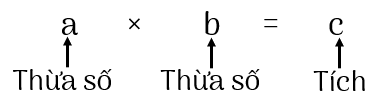
Phép nhân hai số tự nhiên $a$ và $b$ cho ta một số tự nhiên gọi là tích của $a$ và $b$, kí hiệu $a \times b$ hoặc $a.b$ :
$a.b=a+a+a+...+a$ ($b$ số hạng).
Ví dụ: $5 . 4 = 5 + 5 + 5 + 5 = 20$.
Chú ý: Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số. Chẳng hạn, $a.b=ab$ ; $2.m=2m$ .
Ví dụ 1. Đặt tính nhân: $738 . 48$
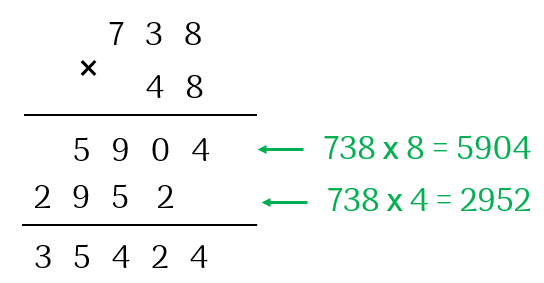
b.Tính chất của phép nhân
Phép nhân có các tính chất:
+ Giao hoán: $ab=ba$.
+ Kết hợp: $(ab)c=a(bc)$.
+ Nhân với số $1$: $a.1=1.a=a$.
+ Phân phối của phép nhân đối với phép cộng và phép : $a(b+c)=ab+ac$.
$a(b-c)=ab-ac$.
Chú ý: Tích $(ab)c$ hay $a(bc)$ gọi là tích của ba số $a$, $b$, $c$ và viết gọn là $abc$.
Ví dụ 2. Tính nhẩm: $24 . 25$
Lời giải. $24 . 25 = (6 . 4). 25 = 6 . (4 . 25) = 6 . 100 = 600$.
Ví dụ 3. Tính nhanh: $54\, 789 . 234 + 54\, 789. 766$.
Lời giải.
$54\, 789. 234 + 54\, 789.766 = 54\, 789. (234+766)$
$=54\, 789. 1\, 000$
$=54\, 789\, 000$.
2. PHÉP CHIA HẾT VÀ PHÉP CHIA CÓ DƯ
Chia hai số tự nhiên
Với hai số tự nhiên $a$ và $b$ đã cho ( $b$ khác 0), ta luôn tìm được đúng hai số tự nhiên $q$ và $r$ sao cho $a=b.q+r$, trong đó $0 \le r <b$.
Nếu $r = 0$ thì ta có phép chia hết $a : b = q$; $a$ là số bị chia, $b$ là số chia, $q$ là thương.
Nếu $r \ne 0$ thì ta có phép chia có dư $a : b = q$ (dư $r$ ); $a$ là số bị chia, $b$ là số chia, $q$ là thương và $r$ là số dư.
Chú ý: Trong phép chia có dư, số dư bao giờ cũng nhỏ hơn số chia.
Ví dụ 4. Đặt tính rồi thực hiện các phép chia sau:
a. $4 \, 847 : 131$.
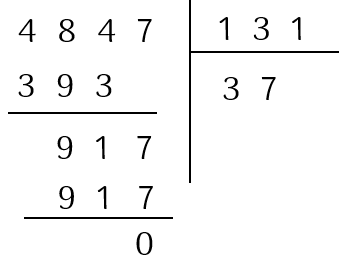
Vậy, $4 \, 847 : 131 = 37$
b. $5 \, 580 : 157$.
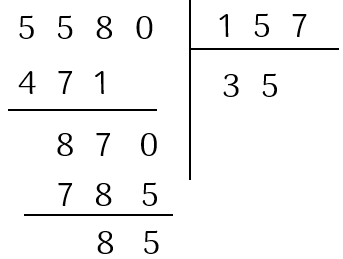
Vậy, $5 \, 580 : 157 = 35$ (dư $85$).
Ví dụ 5. Phải dùng ít nhất bao nhiêu xe ô tô $45$ chỗ ngồi để trở hết $2 \, 457$ cổ động viên của một đội bóng?
Lời giải
Vì $2 \, 457 : 45 = 54$ (dư $27$) nên xếp đủ $54$ xe thì còn thừa $27$ người và phải dùng thêm một xe nữa để chở nốt những người này.
Vậy cần dùng ít nhất $54 + 1 = 55$ (xe).
Bạn có thể đăng câu hỏi về bài học này ở đây