Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (1,5 điểm)
1) Qua điều tra, một lớp học ở trường THCS gồm $40$ học sinh thi khảo sát chất lượng môn Toán có kết quả dạng bảng ghép nhóm như sau:
Nhóm | $[0; 2) $ | $[2; 4)$ | $[4; 6) $ | $[6; 8) $ | $[8; 10)$ |
Số học sinh | $2 $ | $5 $ | $12 $ | $18 $ | $3$ |
Hãy cho biết tần số và tần số tương đối của nhóm $[6; 8)$?
2) Có $15$ quả bi-a giống nhau và ghi số lần lượt từ số $1$ đến $15$ trong hộp kín. Bạn Kẹo lấy ngẫu nhiên một quả bi-a trong hộp. Xét biến cố M: “Kẹo lấy được quả bi-a trong hộp có ghi là số nguyên tố”. Tính xác suất của biến cố $M$.
Hướng dẫn giải:
a) Tần số của nhóm $[6; 8)$ là $18$.
Tần số tương đối của của nhóm $[6; 8)$: $\dfrac{18.100}{40} \%=45\%$.
b) Không gian mẫu của phép thử là: $\Omega = \{1;2;3;...;15\}$.
Vậy không gian mẫu có $15$ phần tử hay $n(\Omega)= 15$.
Các quả bi ghi số nguyên tố là $\{2; 3; 5; 7; 11; 13\}$ nên số các kết quả thuận lợi của biến cố $M$ là $n(M) = 6$.
Vậy xác xuất của biến cố $M$ là $P(M) = \dfrac{n(M)}{n(\Omega)} =\dfrac{6}{15} = \dfrac25$.
Bài 2. (1 điểm) Cho phương trình $x^2 - (m-2)x-3 = 0$ với $x$ là ẩn số, $m$ là tham số. Tìm các giá trị của $m$ để phương trình đã cho có hai nghiệm phân biệt $x_1$ và $x_2$ thỏa mãn điều kiện:
$\sqrt{x_1^2 + 2\,025} - x_1 + (m-3)x_2 + 3 = \sqrt{x_2^2 + 2\,025} - x_2^2$.
Hướng dẫn giải:
Xét phương trình $x^2 -(m-2)x-3=0$.
Ta có: $\Delta=(m-2)^2 + 4.3> 0$ với mọi $m$.
Suy ra phương trình luôn có hai nghiệm phân biệt $x_1$, $x_2$ với mọi $m$.
Theo bài ra ta có:
$\sqrt{x_1^2 +2\,025}-x_1 +(m-3)x_2 +3=\sqrt{x_2^2 +2\,025} +x_2^2$
$\sqrt{x_1^2 +2\,025}- \sqrt{x_2^2 +2\,025}=x_2^2-(m-2)x_2 -3+x_1 +x_2$
$\sqrt{x_1^2 +2\,025}- \sqrt{x_2^2 +2\,025} = x_1 + x_2$ (1)
Do $\sqrt{x_1^2 +2\,025}+ \sqrt{x_2^2 +2\,025} \ne 0$ với mọi $x_1; x_2$, nên nhân cả 2 vế của (1) với $\sqrt{x_1^2 +2\,025} + \sqrt{x_2^2 +2\,025}$ ta được:
$(x_1+x_2)(x_1-x_2)=(x_1 +x_2 )(\sqrt{x_1^2+2\,025}+\sqrt{x_2^2+2\,025})$
$x_1+x_2 =0$ hoặc $\sqrt{x_1^2 +2\,025} + \sqrt{x_2^2 +2\,025}=x_1 -x_2$
+) Với $x_1 +x_2 =0$ suy ra $m-2=0$ hay $m=2$.
+) Với $\sqrt{x_1^2 +2\,025} + \sqrt{x_2^2 +2\,025}=x_1 -x_2$ (2). Cộng vế với vế (1) và (2), ta được: $\sqrt{x_1^2 +2\,025} =x_1$. Phương trình vô nghiệm.
Vậy $m = 2$ thỏa mãn yêu cầu đề bài.
Bài 3. (1 điểm) Giải bài toán sau bằng cách lập phương trình:
Lúc $6$ giờ $30$ phút, một ca nô xuôi dòng sông từ $A$ đến $B$ dài $48$ km. Khi đến $B$, ca nô nghỉ $30$ phút sau đó lại ngược dòng từ $B$ về $A$ lúc $10$ giờ $36$ phút cùng ngày. Tìm vận tốc riêng của ca nô, biết vận tốc dòng nước là $3$ km/h.
Hướng dẫn giải:
Đổi $30$ phút $ = \dfrac12$ giờ;
Ca nô đi hết $10$ giờ $36$ phút - $6$ giờ $30$ phút = $4$ giờ $6$ phút $= \dfrac{41}{10}$ giờ.
Gọi vận tốc riêng của ca nô là $x$ (đơn vị: km/h) $(x > 3)$
Vận tốc ca nô đi xuôi dòng là $x + 3$ (km/h)
Vận tốc ca nô đi ngược dòng là $x - 3$ (km/h)
Thời gian ca nô đi xuôi dòng là $\dfrac{48}{x + 3}$ (h)
Thời gian ca nô đi ngược dòng là $\dfrac{48}{x - 3}$ (h)
Theo đề bài ta có phương trình $\dfrac{48}{x+3}+\dfrac{1}{2}+\dfrac{48}{x-3}=\dfrac{41}{10}$
$\dfrac{48}{x+3}+\dfrac{48}{x-3}=\dfrac{18}{5}$
$\dfrac{48(x-3)+48(x+3)}{(x-3)(x+3)}=\dfrac{18}{5}$
$\dfrac{96x}{(x-3)(x+3)}=\dfrac{18}{5}$
$3x^2-80x-27=0$
$x=\dfrac{-1}{3}$ (không thỏa mãn) hoặc $x=27$ (thỏa mãn).
Vậy vận tốc riêng của ca nô là $27$ km/h.
Bài 4. (2,5 điểm) Cho $(O; R)$ đường kính $AB$. Bán kính $CO$ vuông góc với $AB$, $M$ là điểm bất kì trên cung nhỏ $AC$ ($M$ khác $A$ và $C$), $MB$ cắt $AC$ tại $H$. Gọi $K$ là hình chiếu của $H$ trên $AB$.
a) Chứng minh bốn điểm $C$, $B$, $H$, $K$ cùng thuộc một đường tròn.
b) Chứng minh $CA$ là phân giác góc $MCK$.
c) Kẻ $Ax$ là tiếp tuyến của nửa đường tròn tại $A$. Lấy $P \in Ax$ sao cho $\dfrac{AP. MB}{MA} = R$
Chứng minh $PB$ đi qua trung điểm của đoạn thẳng $HK$.
Hướng dẫn giải:

a) Gọi $I$ là trung điểm của $HB$
Suy ra $HI = IB = \dfrac{HB}{2}$
Xét nửa đường tròn $(O)$, đường kính $AB$ có: $\widehat{ACB} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn)
Suy ra $\Delta CHB$ vuông, mà $CI$ là đường trung tuyến ứng với cạnh huyền
Suy ra $IC = IH = IB = \dfrac{HB}{2}$ (1)
Vì $K$ là hình chiếu của $H$ trên $AB$ nên $\widehat{HKB} = 90^\circ$
Suy ra $\Delta KHB$ vuông, mà $KI$ là đường trung tuyến ứng với cạnh huyền
Suy ra $IK = IH = IB = \dfrac{HB}{2}$ (2)
Từ (1) và (2) suy ra $IC = IK = IH = IB $.
Vậy bốn điểm $C$, $B$, $H$, $K$ cùng thuộc một đường tròn.
b) Có $\widehat{MCA} = \widehat{MBA}$ (góc nội tiếp cùng chắn cung $AM$)
$\widehat{ACK} = \widehat{MBA}$ (tứ giác $CHKB$ nội tiếp)
Suy ra $\widehat{MCA} = \widehat{ACK}$
Suy ra $CA$ là phân giác $\widehat{MCK}$
c) Theo giả thiết: $\dfrac{AP.MB}{MA} = R$
Suy ra $\dfrac{AP}{MA} = \dfrac{OA}{MB}$
Xét $\Delta PAO$ và $\Delta AMB$ có:
$\dfrac{AP}{MA} = \dfrac{OA}{MB}$;
$\widehat{PAO}= \widehat{AMB} = 90^\circ$
Suy ra $\Delta PAO \backsim \Delta AMB$ (c.g.c)
$\widehat{POA}= \widehat{MBA} $ (hai góc tương ứng)
Suy ra $OP$ // $BQ$.
Xét $\Delta ABO$ có: $OP$ // $BO$, $O$ là trung điểm của $AB$ nên $P$ là trung điểm của $AQ$.
Xét $\Delta ABP$ có: $FK$ // $AP$ nên $\dfrac{FK}{AP} = \dfrac{BF}{BP}$
Xét $\Delta ABP$ có: $FK$ // $AP$ nên $\dfrac{FH}{QP} = \dfrac{BF}{BP}$
Từ đó suy ra $HK = FK$ hay $PB$ đi qua trung điểm của đoạn thẳng $HK$.
Bài 5. (1 điểm) Một khối đồ chơi gồm hai khối trụ $(H_1)$, $(H_2)$ xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là $r_1$ =, $h_1$, $r_2$, $h_2$ thỏa mãn $r_2 = \dfrac 12 r_1$, $h_2 = 2h_1$ (tham khảo hình vẽ).
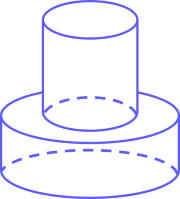
Biết rằng thể tích của toàn bộ khối đồ chơi bằng $30$ (cm3). Tính thể tích khối trụ $(H_1)$.
Hướng dẫn giải:
Thể tích khối $(H_1)$ là $V_1 = \pi .r_1^2. h_1$
Thể tích khối $(H_2)$ là $V_2 = \pi . r_2^2. h_2 = \pi . \dfrac14 . r_1^2. 2. h_1 = \dfrac12 . \pi .r_1^2 .h_1 = \dfrac12 V_1$
Mà $V_1 + V_2 = 30$
$V_1 + \dfrac12 V_1 = 30$
$V_1 = 20$ (cm3).
Vậy thể tích khối $(H_1)$ là $20$ cm3.
Bài 6. (1 điểm) Một trang trại nuôi $100$ con gà. Mỗi con gà đẻ trung bình $250$ quả trứng mỗi năm. Giá bán mỗi quả trứng là $3\,000$ đồng. Chủ trang trại nhận thấy có thể tăng số lượng gà để tăng doanh thu khi bán trứng nên chủ trang trại đã nuôi thêm một số con gà nữa. Nhưng với mỗi một con gà tăng thêm thì số trứng thu về trên mỗi con lại giảm $2$ quả so với trước do ảnh hưởng về điều kiện sống (coi mỗi con gà đẻ được số trứng như nhau). Hỏi nên bổ sung ít nhất bao nhiêu con gà để doanh thu từ bán trứng đạt cao nhất? Tính doanh thu tối đa có thể đạt được.
Hướng dẫn giải:
Gọi số gà cần bổ sung là $x$ (con) ($x \in \mathbb{N}$)
Tổng số gà sau khi bổ sung: $100+x$ (con)
Sản lượng trung bình mỗi con: $250-2x$ (quả)
Tổng số trứng: $(100+x)(250-2x)$ (quả)
Doanh thu: $R(x)=3\,000.(100+x)(250-2x)$ (đồng)
Ta có:
$ T(x)=(100+x)(250-2x) $
$ =-2x^2+50x+25\,000$
$ =-2\Big(x-\dfrac{25}{2}\Big)^2+25\,312,5 $
Để doanh thu $R(x)$ lớn nhất thì $T(x)$ phải đạt giá trị lớn nhất.
Để $T(x)$ phải đạt giá trị lớn nhất khi và chỉ khi $\Big(x-\dfrac{25}{2}\Big)^2$ đạt giá trị nhỏ nhất với $x$ là số tự nhiên, $x$ nhỏ nhất.
Suy ra tìm được $x=12.$
Vậy số gà ít nhất cần bổ sung để đạt doanh thu cao nhất là $12$ con.
Vậy doanh thu tối đa là: $R(12)=3\,000.(100+12)(250-2.12)=75\,936\,000$ đồng.
