Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (8 điểm) SVIP
Bài 1. (1,5 điểm) Cho phương trình: $x^2-2mx+m^2-1=0$ (1) ($m$ là tham số).
a) Giải phương trình (1) với $m=2$.
b) Tìm $m$ để phương trình có hai nghiệm phân biệt $x_1$; $x_2$ (với $x_1<x_2$) thỏa mãn $2x_1^2-x_2=-2$.
Hướng dẫn giải:
a) Với $m=2$, phương trình (1) trở thành:
$x^2-4x+3=0$
Vì $a+b+c=1-4+3=0$ nên $x_1=1$ và $x_2=3$.
Vậy với $m=2$, phương trình có hai nghiệm là $x_1=1$ và $x_2=3$.
b) Vì $a=1\ne 0$ nên phương trình đã cho là phương trình bậc hai.
Ta có: $\Delta '=(-m)^2-(m^2-1)=1$
Vì ${\Delta }'=1>0$ với mọi giá trị của $m$ nên phương trình đã cho luôn có hai nghiệm phân biệt với mọi giá trị của $m$, hai nghiệm đó là: $m-1$ và $m+1$.
Vì $x_1<x_2$ nên $x_1=m-1$ và $x_2=m+1$
Thay $x_1=m-1$ và $x_2=m+1$ vào đẳng thức $2x_1^2-x_2=-2$ ta được:
$2(m-1)^2-(m+1)=-2$
$2m^2-5m+3=0$
Vì $2+(-5)+3=0$ nên $m_1=1$; $m_2=\dfrac{3}{2}$
Vậy $m\in \Big\{ 1;\dfrac{3}{2} \Big\}$.
Bài 2. (1,5 điểm) Tại một trại hè thanh thiếu niên quốc tế, người ta tìm hiểu xem mỗi đại biểu tham dự có thể sử dụng được bao nhiêu ngoại ngữ. Kết quả được như bảng sau:
Số ngoại ngữ | $1$ | $2$ | $3$ | $4$ | $\ge 5$ |
Số đại biểu | $84$ | $64$ | $24$ | $16$ | $12$ |
a) Hãy lập bảng tần số tương đối ở bảng trên.
b) Hãy tính tỉ lệ phần trăm đại biểu sử dụng được ít nhất $2$ ngoại ngữ.
c) Tại trại hè thanh thiếu niên quốc tế tổ chức $1$ năm trước đó, có $54$ trong tổng số $220$ đại biểu tham dự có thể sử dụng được từ $3$ ngoại ngữ trở lên. Có ý kiến cho rằng “Tỉ lệ đại biểu sử dụng được $3$ ngoại ngữ trở lên có tăng giữa hai năm đó”. Ý kiến đó đúng hay sai?
Hướng dẫn giải:
a) Bảng tần số tương đối:
Số đại biểu | $84$ | $64$ | $24$ | $16$ | $12$ |
Tần số tương đối | $42\%$ | $32\%$ | $12\%$ | $8\%$ | $6\%$ |
b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất $2$ ngoại ngữ là:
$32\% + 12\% + 8\% + 6\% = 58\%$.
c) Ý kiến đó đúng vì:
+ Tỉ lệ đại biểu sử dụng được $3$ ngôn ngữ của $1$ năm trước là: $24,5\%$.
+ Tỉ lệ đại biểu sử dụng được $3$ ngôn ngữ của năm nay là:
$12\% + 8\% + 6\% = 26\% > 24,5\%$.
Một hộp có $20$ viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số $1; 2; 3 ; ... 20$; hai viên bi khác nhau thì viết hai số khác nhau.
Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp".
a) Viết không gian mẫu phép thử đó.
b) Tính xác suất biến cố: “Số xuất hiện trên viên bi được lấy ra chia $7$ dư $1$".
Hướng dẫn giải:
a) Các kết quả có thể xảy ra là: $1$; $2$; $3$; $4$; ... ; $18$; $19$; $20$.
$\Omega = \{1; 2; 3; 4; ... ; 18; 19; 20\}$.
b) Có $3$ kết quả thuận lợi cho biến cố $T$ là $1, 8, 15$.
Vậy $P(T)=\dfrac{3}{20}=0,15$.
Bài 4. (1 điểm) Mặt xung quanh của một thùng chứa nước hình trụ có chiều cao 1 m được gõ từ một tấm tôn hình chữ nhật có kích thước $1$ m x $2$ m (như hình vẽ).
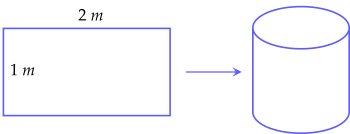
a) Hỏi thùng nước này đựng đầy được bao nhiêu mét khối nước?
(Bỏ qua bề dày của thùng nước và lấy $\pi =3,14$ làm tròn đến chữ số thập phân thứ hai).
b) Một em bé đánh rơi quả bóng bưởi xuống thùng tôn. Bên cạnh có một vòi nước cung cấp nước. Em bé cần lấy ít nhất bao nhiêu nước từ vòi để lấy được bóng?
Hướng dẫn giải:
a) Thùng nước là một hình trụ có chiều cao $h=1$ m, chu vi đáy là $C=2$ m.
Gọi $R$ là bán kính đáy của hình trụ
Ta có : $C=2\pi .R$, suy ra $R=\dfrac{1}{\pi }$ (m)
Thể tích của hình trụ là : $V=\pi R^2h=\pi \Big( \dfrac{1}{{{\pi }^{2}}} \Big).1=\dfrac{1}{\pi }\approx 0,32$ m3.
Vậy thùng đựng được $0,32$ m3 nước.
b) Để lấy bóng, em bé chỉ cần đổ đầy nước vào thùng tôn. Em bé cần lấy ít nhất $0,32$ m3 nước thì bóng nổi trên mặt thùng tôn khi đó sẽ an toàn.
Bài 5. (2,5 điểm) Cho đường tròn $(O;R)$ có hai đường kính $AB$ và $CD$ vuông góc tại $O$. Gọi là $I$ trung điểm của $OB$. Tia $CI$ cắt đường tròn $(O)$ tại $E$. Gọi $H$ là giao điểm của $AE$ và $CD$.
a) Chứng minh bốn điểm $O$, $I$, $E$, $D$ cùng thuộc một đường tròn.
b) Chứng minh: $AH.AE = 2R^2$ và $OA = 3OH$.
c) Gọi $K$ là hình chiếu của $O$ trên $BD$, $Q$ là giao điểm của $AD$ và $BE$. Chứng minh: $Q$, $K$, $I$ thẳng hàng.
Hướng dẫn giải:

a) Gọi $J$ là trung điểm của $ID$
+) $AB$ vuông góc $CD$ tại $O$, mà $I\in OB$
Suy ra $\widehat{IOD}=90^\circ $
$\Delta IOD$ vuông tại $O$, từ đó suy ra : $JO=JI=JD$(1)
+ Ta có: $\widehat{CED}$ là góc nội tiếp chắn nửa đường tròn, nên $\widehat{CED}=90^\circ $
Hay $\widehat{IED}=90^\circ $, suy ra $\Delta IED$ vuông tại $E$,
Suy ra $JI=JE=JD$ (2)
Từ (1) và (2) suy ra $O$, $I$, $E$, $D$ cùng thuộc một đường tròn đường kính $ID$.
b) Xét $\Delta AHO$ và $\Delta ABE$ có:
$\widehat{AOH}=\widehat{AEB}=90^\circ $;
$\widehat{A}$: góc chung
Do đó $\Delta AHO\backsim \Delta ABE$ (g.g)
Suy ra: $\dfrac{AH}{AB}=\dfrac{AO}{AE}$
Hay $AH.AE=AO.AB$
Suy ra $AH.AE=2R^2$ (điều phải chứng minh)
+) Từ $\Delta AHO\backsim \Delta ABE$ suy ra: $\dfrac{OA}{AE}=\dfrac{OH}{BE}$ hay $\dfrac{OA}{OH}=\dfrac{AE}{BE}$
Mà $EI$ là tia phân giác của góc $AEB$nên suy ra:
$\dfrac{AE}{BE}=\dfrac{AI}{IB}=\dfrac{\dfrac{3}{2}R}{\dfrac{1}{2}R}=3$
Suy ra $\dfrac{OA}{OH}=\dfrac{1}{3}$
Do đó, $OA=3OH$.
c) Vì $OA=3OH$, mà $OA=OD(=R)$ nên $OD=3OH$
Suy ra $HD=\dfrac{2}{3}OD$
Suy ra $H$ là trọng tâm tam giác $ABD$.
$AB\bot CD$ nên $\widehat{BOD}=90^\circ $
$\Delta OBD$ vuông tại $O$ có $OB=OD(=R)$ nên là tam giác vuông cân tại $O$ có đường cao $OK$ đồng thời là đường trung tuyến nên $K$ là trung điểm của $DB$.
Suy ra $A$, $H$, $K$, $E$ thẳng hàng
Ta có $AE$ cắt $BD$ tại $K$ nên $K$ là trực tâm của $\Delta ABQ$
$KQ\bot AB$ (3)
$\Delta OKB$ có $OK=OB$ (Vì $OK$ là trung tuyến ứng với cạnh huyền trong tam giác vuông cân $ABD$) nên $\Delta OKB$ cân tại $K$.
Suy ra $KI$ là đường trung tuyến đồng thời là đường cao, hay $KI\bot OB$
Suy ra $KI\bot AB$ (4)
Từ (3) và (4) suy ra $Q$, $K$, $I$ thẳng hàng. (điều phải chứng minh).
Bài 4. (1 điểm) Mặt xung quanh của một thùng chứa nước hình trụ có chiều cao 1 m được gõ từ một tấm tôn hình chữ nhật có kích thước $1$ m x $2$ m (như hình vẽ).

a) Hỏi thùng nước này đựng đầy được bao nhiêu mét khối nước?
(Bỏ qua bề dày của thùng nước và lấy $\pi =3,14$ làm tròn đến chữ số thập phân thứ hai).
b) Một em bé đánh rơi quả bóng bưởi xuống thùng tôn. Bên cạnh có một vòi nước cung cấp nước. Em bé cần lấy ít nhất bao nhiêu nước từ vòi để lấy được bóng?
Hướng dẫn giải:
Đặt $AE=x$ ($0\le x\le 30$)
Chỉ ra được ${{S}_{EFGH}}={{S}_{ABCD}}-4{{S}_{AEH}}=900-2x(30-x)$
Do đó $2x^2-60x+900=2(x-15)^2+450 \ge 450$
Dấu “$=$" xảy ra khi và chỉ khi $x=15$ (TM)
Vậy $\min {{S}_{EFGH}}=450$ m2 khi $AE=15$.
