Phần tự luận (3 điểm) SVIP

Hướng dẫn giải:

Gọi $A$ là số tiền tối đa người này có thể vay, ${{A}_{i}}$ là số tiền nợ sau tháng thứ $i$. (đơn vị: triệu đồng)

${{r}_{1}}=\dfrac{5\%}{12}$ là lãi suất/1 tháng, trong $6$ tháng đầu

${{r}_{2}}=\dfrac{12\%}{12}=1\%$ là lãi suất/1 tháng, từ tháng thứ 7 trở đi.

Sau 1 tháng, số tiền gốc và lãi là $A(1+r)$, người đó trả $15$ triệu nên còn nợ:

${{A}_{1}}=A(1+r)-15$

Sau tháng thứ 2:

${{A}_{2}}={{A}_{1}}(1+{{r}_{1}})-15$

$=(A(1+{{r}_{1}})-15)(1+{{r}_{1}})-15$

$=A{{(1+{{r}_{1}})}^{2}}-\dfrac{15}{{{r}_{1}}}\left[ {{(1+{{r}_{1}})}^{2}}-1 \right]$

Sau tháng thứ 3:

${{A}_{3}}=A{{(1+{{r}_{1}})}^{3}}-\dfrac{15}{{{r}_{1}}}\left[ {{(1+{{r}_{1}})}^{3}}-1 \right]$

…….

Sau tháng thứ 6:

${{A}_{6}}=A{{(1+{{r}_{1}})}^{6}}-\dfrac{15}{{{r}_{1}}}\left[ {{(1+{{r}_{1}})}^{6}}-1 \right]$.

Sau tháng thứ 7: ${{A}_{7}}={{A}_{6}}(1+{{r}_{2}})-15$

Sau tháng thứ 8: ${{A}_{8}}={{A}_{6}}{{(1+{{r}_{2}})}^{2}}-\dfrac{15}{{{r}_{2}}}\left[ {{(1+{{r}_{2}})}^{2}}-1 \right]$

………

Sau tháng thứ $240$ (sau đúng $20$ năm):

${{A}_{240}}={{A}_{6}}{{(1+{{r}_{2}})}^{234}}-\dfrac{15}{{{r}_{2}}}\left[ {{(1+{{r}_{2}})}^{234}}-1 \right]$

Vì phải trả hết nợ sau $20$ năm nên:

${{A}_{240}}=0$

$\Leftrightarrow {{A}_{6}}=\dfrac{15\left[ {{(1+{{r}_{2}})}^{234}}-1 \right]}{{{(1+{{r}_{2}})}^{234}}{{r}_{2}}}\approx 1\,353,819328$

$\Rightarrow A=\dfrac{{{A}_{6}}+\dfrac{15}{{{r}_{1}}}\left[ {{(1+{{r}_{1}})}^{6}}-1 \right]}{{{(1+{{r}_{1}})}^{6}}}\approx 1\.409,163992$.

Vậy người này có thể mua được căn nhà có giá trị tối đa là $\dfrac{A}{85\%}\approx 1\,657,83999$ triệu đồng$\approx 1,65784$ tỷ đồng.

Hướng dẫn giải:

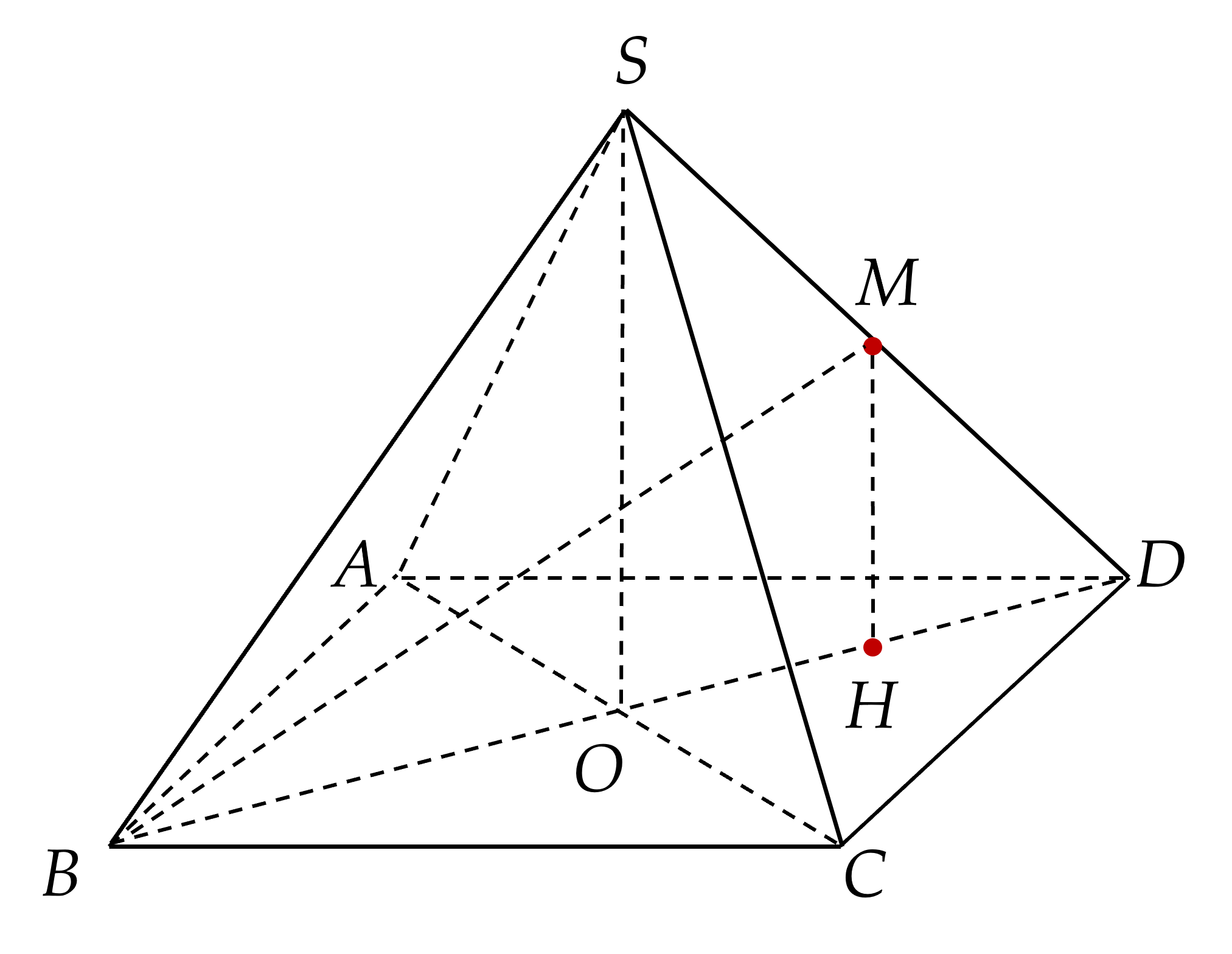
 Gọi $O=AC\cap BD$

$\Rightarrow SO\bot (ABCD)$. Gọi $H$ trung điểm của $OD$.

Xét $\Delta SOD$, $MH$ là đường trung bình

$\Rightarrow MH\parallel SO$ $\Rightarrow MH\bot (ABCD)$.

Hình chiếu của đường thẳng $BM$ trên mặt phẳng $(ABCD)$ là $BH$.

$\Rightarrow \widehat{(BM;(ABCD))}=\widehat{(BM;BH)}=\widehat{MBH}$

Xét tam giác vuông $ABD$ có $BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}$$=\sqrt{{{(2a)}^{2}}+{{(2a)}^{2}}}$$=2\sqrt{2}a$.

$\Rightarrow BH=\dfrac{3}{4}BD=\dfrac{3\sqrt{2}a}{2}$ và $OD=\dfrac{1}{2}BD=\sqrt{2}a$.

Xét tam giác vuông $SOD$ có:

$SO=\sqrt{S{{D}^{2}}-O{{D}^{2}}}$

$=\sqrt{{{(2a)}^{2}}-{{(\sqrt{2}a)}^{2}}}$

$=\sqrt{2}a$.

$\Rightarrow MH=\dfrac{1}{2}SO=\dfrac{\sqrt{2}a}{2}$.

Ta có: $\tan \widehat{MBH}=\dfrac{MH}{BH}$

$=\dfrac{\dfrac{a\sqrt{2}}{2}}{\dfrac{3\sqrt{2}a}{2}}$

$=\dfrac{1}{3}$.

Hướng dẫn giải:

Điều kiện $\left\{ \begin{aligned}& x>0 \\& {{5}^{x}}-m\ge 0 \\\end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}& x>0 \\& m\le {{5}^{x}} \\\end{aligned} \right.$.

$(2\log _{3}^{2}x-{{\log }_{3}}x-1)\sqrt{{{5}^{x}}-m}=0$

$\Leftrightarrow \left\{ \begin{aligned}& x>0,\ {{5}^{x}}-m\ge 0 \\& \left[ \begin{aligned}& {{5}^{x}}-m=0 \\& 2\log _{3}^{2}x-{{\log }_{3}}x-1=0 \\\end{aligned} \right. \\\end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}& x>0,\ {{5}^{x}}-m\ge 0 \\& \left[ \begin{aligned}& {{5}^{x}}-m=0 \\& {{\log }_{3}}x=\dfrac{-1}{2} \\& {{\log }_{3}}x=1 \\\end{aligned} \right. \\\end{aligned} \right.$

$\Leftrightarrow \left\{ \begin{aligned}& x>0,{{5}^{x}}-m\ge 0 \\& \left[ \begin{aligned}& x={{\log }_{5}}m \\& x={{3}^{\frac{1}{\sqrt{2}}}} \\& x=3 \\\end{aligned} \right. \\\end{aligned} \right.$

+ Khi $m=1\Rightarrow x={{\log }_{2}}1=0$.

Vậy phương trình $(2 \log _{3}^{2} x-\log _{3} x-1) \sqrt{5^{x}-m}=0$ có 2 nghiệm $\left[ \begin{aligned}& x={{3}^{\frac{1}{\sqrt{2}}}} \\& x=3 \\\end{aligned} \right.$

+ $m>1\Rightarrow x={{\log }_{5}}m$ là 1 nghiệm.

Để phương trình có đúng 2 nghiệm thì $\dfrac{1}{\sqrt{3}}\le {{\log }_{5}}m<3$

$\Leftrightarrow {{5}^{\frac{1}{\sqrt{3}}}}\le m<{{5}^{3}}$

$\Leftrightarrow 2,53\le m<125$.