Phần tự luận (3 điểm) SVIP

Hướng dẫn giải:

Với $a$ (triệu đồng) là số tiền ông Đại đóng vào hằng tháng, $r%$ lãi suất ông Đại gửi tiết kiệm hằng tháng.

Gọi ${{P}_{n}}$ là số tiền mà ông Đại thu được sau $n$ tháng $(n\ge 1)$.

Suy ra

${{P}_{1}}=a.(1+r\%)$.

${{P}_{2}}=({{P}_{1}}+a)(1+r\%)=a.{{(1+r\%)}^{2}}+a.(1+r\%)$

${{P}_{3}}=({{P}_{2}}+a)(1+r\%)=a.{{(1+r\%)}^{3}}+a.{{(1+r\%)}^{2}}+a.(1+r\%)$

……………………………………………………………………….

${{P}_{n}}=({{P}_{n-1}}+a)(1+r\%)=a.{{(1+r\%)}^{n}}+a.{{(1+r\%)}^{n-1}}+...+a.(1+r\%)$

Xét cấp số nhân có số hạng đầu là ${{u}_{1}}=a.(1+r\%)$ và công bội $q=1+r\%$ thì ${{P}_{n}}={{u}_{1}}+{{u}_{2}}+...+{{u}_{n}}={{u}_{1}}\dfrac{1-{{q}^{n}}}{1-q}$.

Vậy số tiền ông Đại nhận được từ ngân hàng sau $5$ năm ($60$ tháng) là

${{P}_{60}}={{u}_{1}}\dfrac{1-{{q}^{60}}}{1-q}=5.(1,0033).\dfrac{1-{{(1,0033)}^{60}}}{0,0033}\approx 332$ triệu đồng.

Hướng dẫn giải:

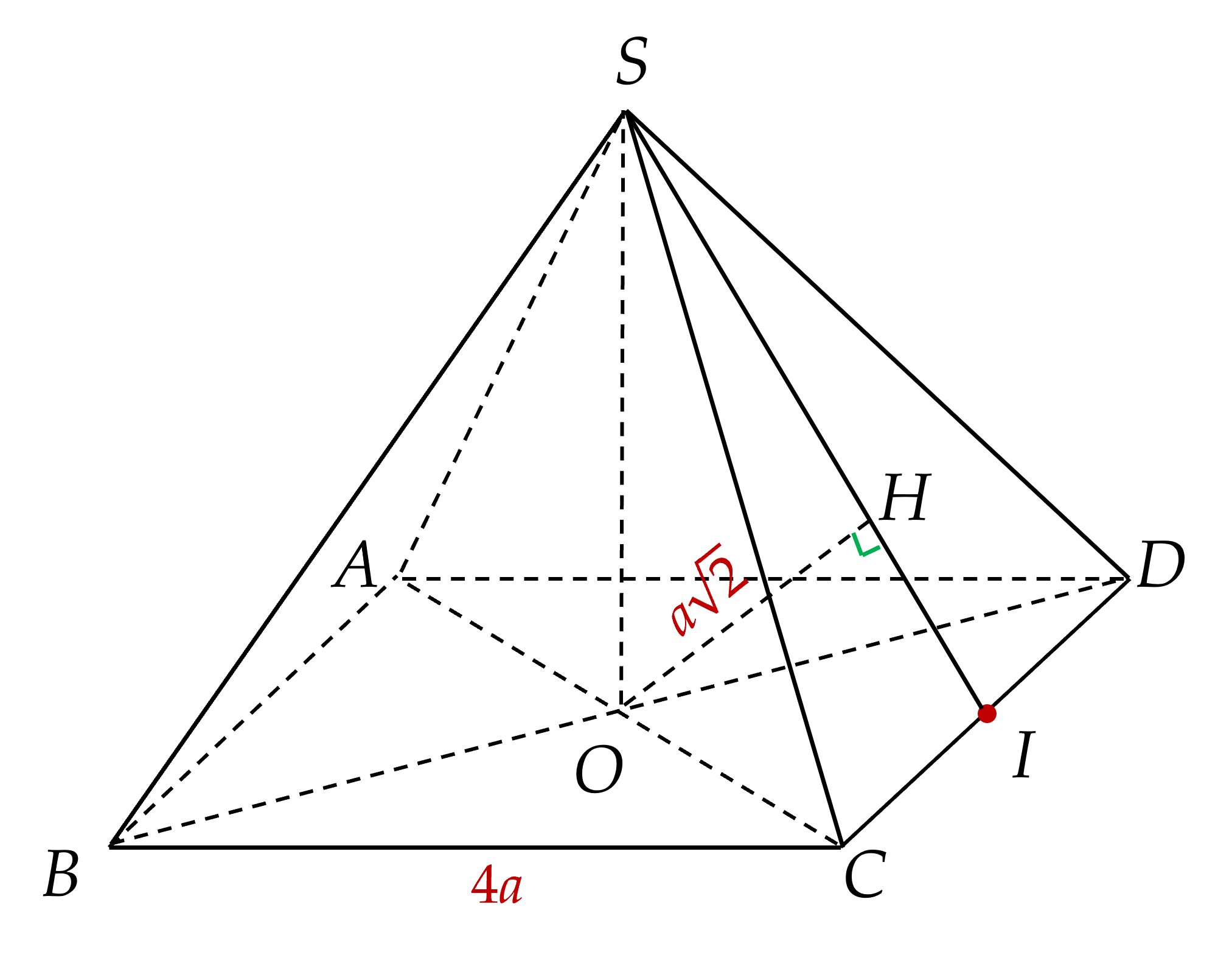
Ta có: $\left. \begin{aligned}& SO\bot (ABCD) \\& CD\subset (ABCD) \\\end{aligned} \right\}\Rightarrow SO\bot CD,\,OI\bot CD\Rightarrow CD\bot (SOI)$.

$OH\subset (SOI)\Rightarrow OH\bot CD$,

$OH\bot SI\,\Rightarrow OH\bot (SIO)$

$\Rightarrow (SO,\,(SCD))=\widehat{OSI}$.

$OI=2a,\,OH=a\sqrt{2}\,\Rightarrow \Delta OHI\,$ vuông cân tại $H$

$\Rightarrow \,\widehat{HIO}=\,45^\circ \Rightarrow \widehat{OSI}=45^\circ $.

Xét tam giác $SOD$:

$SD=\sqrt{SO^2+OD^2}=\sqrt{\dfrac{a^2}{2}+\dfrac{a^2}{2}}=a$

$\Rightarrow SD=SC=CD=a$

$\Rightarrow \Delta SCD$ đều

$\Rightarrow \widehat{SDC}=60^\circ $.

Suy ra $(AB,SD)=(CD,SD)=\widehat{SDC}=60^\circ $.

Hướng dẫn giải:

Gọi ${{A}_{i}}$ là biến cố “Xạ thủ thứ $i$ bắn trúng mục tiêu” với $i=1,2$.

Ta có: $P({{A}_{1}})=0,7\Rightarrow P(\overline{{{A}_{1}}})=0,3;\ P({{A}_{2}})=0,8\Rightarrow P(\overline{{{A}_{2}}})=0,2$.

Gọi $X$ là biến cố “Mục tiêu bị bắn trúng”.

$\Rightarrow P(X)=P({{A}_{1}}). P(\overline{{{A}_{2}}})+P({{A}_{2}}). P(\overline{{{A}_{1}}})+P({{A}_{1}}). P({{A}_{2}})$

$=0,7. 0,2+0,8.0,3+0,7.0,8=0,94$.