Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Phần tự luận (3 điểm) SVIP
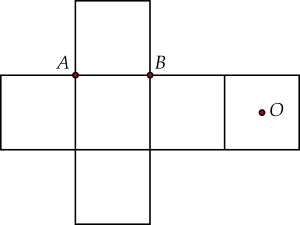
Một hình lập phương được tạo thành khi xếp miếng bìa carton như hình vẽ bên dưới. Khoảng cách từ điểm $O$ đến đường thẳng $AB$ sau khi xếp bằng bao nhiêu? (biết rằng độ dài đoạn thẳng $AB$ bằng $4\sqrt{5}$.)
Hướng dẫn giải:

Sau khi xếp miếng bìa lại ta được hình lập phương $ABCD.A'B'C'D'$ cạnh $4\sqrt{5}$, $O$ là tâm của $A'B'C'D'$.
Gọi $M,\,N$ lần lượt là trung điểm các cạnh $AB,\, A'B'.$
$\Rightarrow MN=AA'=4\sqrt{5}$,
$OM=\dfrac{1}{2}A'D'=2\sqrt{5}$.
Lại có: $\left\{ \begin{aligned}& AB\bot OM \\& AB\bot MN \\\end{aligned} \right.$
$\Rightarrow AB\bot ON$
$\Rightarrow d(O,AB )=ON$
$=\sqrt{OM^2+MN^2}=10$.
Cho khối hộp chữ nhật $ABCD.A'B'C'D'$ có đáy là hình vuông, $BD=2a$, góc giữa hai mặt phẳng $(A'BD )$ và $(ABCD )$ bằng $30^\circ$. Khoảng cách từ A đến mặt phẳng $(A'BD )$ bằng
Hướng dẫn giải:

Gọi $O$ là giao điểm của $AC$ và $BD$.
Ta có $\left\{ \begin{aligned}&AA'\cap AO=A\\&AA',\,AO \subset (AOA')\\& BD\bot AO \\& BD\bot A{A}' \\\end{aligned} \right.$
$\Rightarrow BD\bot (AO{A}')$
$\Rightarrow {A}'O\bot BD$. $\Big($vì $A'O$ nằm trong $(AA'O)\Big)$.
Khi đó $(({A}'BD ),(ABCD ) )=({A}'O,AO )=\widehat{{A}'OA}=30{}^\circ $.
Vẽ $AH\bot {A}'O$ tại $H$.
Ta có $BD\bot (AO{A}' )\Rightarrow ({A}'BD )\bot (AO{A}' )$.
Khi đó $\left\{ \begin{aligned}& (AO{A}' )\bot ({A}'BD ) \\& (AO{A}' )\cap ({A}'BD )={A}'O \\&AH\bot {A}'O \\\end{aligned} \right.$
$\Rightarrow AH\bot ({A}'BD )\Rightarrow d(A,({A}'BD ) )=AH$.
$AC=BD=2a\Rightarrow AO=a$,
$AH=AO.\sin \widehat{AO{A}'}=a.\sin 30{}^\circ =\dfrac{a}{2}$.
Vậy $d(A,({A}'BD ) )=\dfrac{a}{2}$.
Bạn Bình được gia đình gửi vào sổ tiết kiệm $200$ triệu đồng với lãi suất $0,45\%$ một tháng theo hình thức lãi kép. Nếu mỗi tháng Bình rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì hàng tháng Bình rút ra bao nhiêu để đúng $4$ năm vừa hết số tiền trong sổ tiết kiệm?
Hướng dẫn giải:
Gọi số tiền bạn Bình rút ra hàng tháng là $x$ (triệu đồng) $(x>0 )$, số tiền ban đầu là $P$(triệu đồng), $(P>0 )$, lãi suất tiền gửi hàng tháng là $r$, $(r>0 )$.
Lãi suất nhận được sau tháng thứ nhất là: $P.r$ (triệu đồng).
Số tiền cuối tháng thứ nhất sau khi rút còn lại: ${{P}_{1}}=P(1+r )-x$ (triệu đồng).
Lãi suất nhận được sau tháng thứ nhất là: ${{P}_{1}}.r$ (triệu đồng).
Số tiền cuối tháng thứ nhất sau khi rút còn lại:
${{P}_{2}}={{P}_{1}}(1+r )-x=P{{(1+r )}^{2}}-x(1+r )-x$ (triệu đồng).
Cứ như thế, số tiền còn lại sau $n$ tháng là:
${{P}_{n}}=P{{(1+r )}^{n}}-x{{(1+r )}^{n-1}}-x{{(1+r )}^{n-2}}-....-x(1+r )-x$
${{P}_{n}}=P{{(1+r )}^{n}}-x.\dfrac{{{(1+r )}^{n}}-1}{r}$ (triệu đồng).
Sau $48$ tháng, số tiền vừa hết khi và chỉ khi
${{P}_{n}}=0$
$\Leftrightarrow P{{(1+r )}^{48}}-x.\dfrac{{{(1+r )}^{48}}-1}{r}=0$
$\Leftrightarrow 200{{(1,0045 )}^{48}}-x.\dfrac{{{(1,0045 )}^{48}}-1}{0,0045}=0$
$\Leftrightarrow x\approx 4,642$ (triệu đồng).
