Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Kiểm tra cuối chương I SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hàm số y=x3−2x2+x+1. Mệnh đề nào sau đây đúng?
Cho hàm số y=f(x) có đồ thị như hình vẽ.
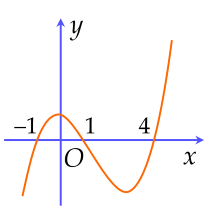
Hàm số đồng biến trên khoảng nào sau đây?
Số điểm cực trị của hàm số y=41x5−2x3+6 là
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
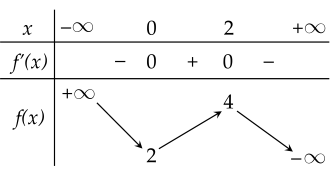
Điểm cực tiểu của đồ thị hàm số là
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x3−3x2−9x+35 trên đoạn [−4;4]. Giá trị của M và m lần lượt là
Cho hàm số y=f(x) có đồ thị như hình vẽ dưới.
![Giá trị lớn nhất của hàm số trên $[ -3;4 ]$ bằng Giá trị lớn nhất của hàm số trên $[ -3;4 ]$ bằng](https://cdn3.olm.vn/upload/img_teacher/0120/img_teacher_2025-01-20_678d3fca71a19.jpg)
Giá trị lớn nhất của hàm số trên [−3;4] bằng
Số đường tiệm cận của đồ thị hàm số y=2x+32x−1 là
Đồ thị hàm số nào sau đây nhận đường thẳng x=2 làm đường tiệm cận đứng?
Cho hàm số hữu tỉ y=ax+2+x+cb có đồ thị như hình sau.

Giá trị của biểu thức P=a+b+c là
Đồ thị hàm số y=2x−12x+1 có tọa độ giao điểm với trục tung là
Hàm số y=∣x3+3x∣ nghịch biến trên khoảng nào dưới đây?
Cho hàm số y=f(x) xác định trên R\{x2} và có bảng xét dấu của đạo hàm như sau:
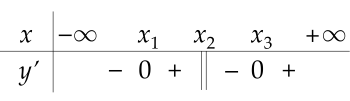
Số điểm cực trị của hàm số y=f(x) là
Số tiệm cận đứng của đồ thị hàm số y=x2−3x+2x2−5x+6 là
Hoành độ giao điểm của đồ thị hàm số y=4−ln(3−x) và trục hoành là
Cho hàm số y=x−23x−2 có đồ thị (C) và đường thẳng d:y=x+1.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) (C) cắt trục hoành tại điểm có hoành độ x=2. |
|
| b) Đường tiệm cận ngang của đồ thị hàm số (C) là y=32. |
|
| c) Giao điểm của (C) với trục tung là N(0;−2). |
|
| d) Đường thẳng d cắt (C) tại hai điểm A và B thì tọa độ trung điểm M của đoạn thẳng AB là M(2;3). |
|
Cho hàm số y=f(x) có đạo hàm f′(x)=(x+2)x(x−2) với mọi x∈R.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số y=f(x) nghịch biến trên khoảng (0;2). |
|
| b) Hàm số y=f(x) đồng biến trên khoảng (−2;0). |
|
| c) Hàm số y=f(x) có hai điểm cực trị. |
|
| d) Hàm số y=f(x) có hai điểm cực tiểu. |
|
Cho hàm số y=x+1x2+2x+5.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) y′=(x+1)2x2+2x−3. |
|
| b) Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là y=2x−2. |
|
| c) Đồ thị hàm số có đường tiệm cận xiên là y=x+1. |
|
d) Đồ thị của hàm số có hình vẽ như sau:

|
|
Cho hàm số f(x)=e2x−2x.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số có tập xác định là R. |
|
| b) Đạo hàm của hàm số đã cho là f′(x)=2e2x−2. |
|
| c) Tập nghiệm của bất phương trình f′(x)>0 là S=(0;+∞). |
|
| d) Hàm số đã cho có giá trị cực tiểu bằng 0. |
|
Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y=(mx2−6x+3)(9x2+6mx+1)6x−3 có đúng một đường tiệm cận?
Trả lời:
Cho hàm số y=x3−3mx+1 (1). Cho A(2;3), giá trị của m để đồ thị hàm số (1) có hai điểm cực trị B và C sao cho tam giác ABC cân tại A bằng bao nhiêu? Làm tròn đến chữ số thập phân thứ nhất.
Trả lời:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau:
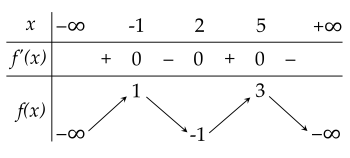
Phương trình f′[5−3f(x)]=0 có bao nhiêu nghiệm thực?
Trả lời:
Cho hàm số y=x3−3mx2+(2m2+1)x−mx−3. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−6;6] để đồ thị hàm số có 4 đường tiệm cận?
Trả lời:
Cho hàm số y=x4−2mx2+4m−4 (m là tham số thực). Giá trị của m bằng bao nhiêu để đồ thị hàm số đã cho có 3 điểm cực trị tạo thành tam giác có diện tích bằng 1?
Trả lời:
