Bài học cùng chủ đề
- Đường thẳng song song với mặt phẳng
- Một số dạng toán về đường thẳng song song với mặt phẳng
- Đường thẳng song song với mặt phẳng
- Tìm thiết diện của mặt phẳng với khối chóp
- Bài tập mẫu: Chứng minh đường thẳng song song với mặt phẳng
- Bài tập mẫu: Dựng mặt phẳng song song với đường thẳng
- Bài tập mẫu: Thiết diện
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Một số dạng toán về đường thẳng song song với mặt phẳng SVIP
Tải đề xuống bằng file Word
1. Tìm giao tuyến.
$*)$ Tính chất
Cho đường thẳng $a$ song song với mặt phẳng $(P)$. Nếu mặt phẳng $(Q)$ chứa a và cắt $(P)$ theo giao tuyến $b$ thì $b$ song song với $a$.
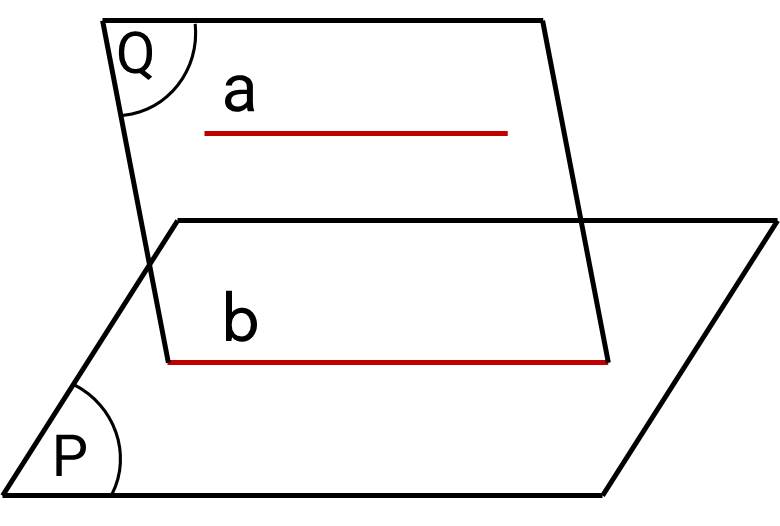
$*)$ Phương pháp:
Ngoài cách tìm ra $2$ điểm chung của $2$ mặt phẳng, ta có thể dựng giao tuyến như sau:
Bước 1: Chỉ ra rằng $(P)$, $(Q)$ lần lượt chứa hai đường thẳng song song $a$ và $b$.
Bước 2: Tìm điểm chung $M$ của hai mặt phẳng.
Bước 3: Giao tuyến của hai mặt phẳng $(P)$ và $(Q)$ là đường thẳng đi qua $M$ và song song với $a$ và $b$.
2. Dựng thiết diện đi qua một điểm và song song với một hoặc hai đường thẳng
Định nghĩa thiết diện: Thiết diện (mặt cắt) là một đa giác phẳng thu được khi cắt một khối chóp bằng một mặt phẳng. (Các cạnh của đa giác thu được là các đoạn giao tuyến của mặt phẳng với mặt bền hoặc mặt đáy của hình chóp).
Vậy để tìm một thiết diện nói chung, ta cần tìm giao tuyến của mặt phẳng với một khối chóp.
Phương pháp: Tìm thiết diện của một hình chóp với một mặt phẳng $(P)$ :
Bước 1: Từ điểm chung có sẵn, xác định giao tuyến đầu tiên của $(P)$ với một mặt của hình chóp (có thể là mặt phẳng trung gian).
Bước 2: Cho giao tuyến vừa tìm được cắt các cạnh của mặt đó của hình chóp, ta sẽ được các điểm chung mới của $(P)$ với các mặt khác. Từ đó xác định được giao tuyến với các mặt này.
Bước 3: Tiếp tục như trên tới khi các giao tuyến khép kín ta được thiết diện.
Chú ý:
+ Thiết diện của một khối chóp là một đa giác bao quanh viền ngoài khối chóp, không có đường thẳng nào đâm xuyên bên trong khối chóp đó.
+ Có thể tìm thiết diện bằng phương pháp dựng giao điểm.
Ví dụ 1: Cho tứ diện $A B C D$, điểm $M$ thuộc $A C$. Xác định thiết diện của tứ diện $A B C D$ cắt bởi mặt phẳng $(\alpha)$ đi qua $M$ song song với $A B$ và $A D$.
Giải
Ta dựng mặt phẳng $(\alpha)$ như sau, trong mặt phẳng $(ABC)$, dựng $MP$ // $AB$ với $P \in BC$, trong mặt phẳng $(ACD)$, dựng $MN$ // $AD$. Vậy $(\alpha) \equiv (MNP)$.
$(ABC) \cap (MNP) = MP$
$(ADC) \cap (MNP) = MN$
$(BCD) \cap (MNP) = NP$
Vậy thiết diện của mặt phẳng $\alpha$ với hình chóp là tam giác $MNP$.
Ví dụ 2: Cho hình chóp $S . A B C D$ có đáy $A B C D$ là tứ giác lồi. Điểm $I$ là giao điểm của hai đường chéo $A C$ và $B D$. Xác định thiết diện của hình chóp $S . A B C D$ cắt bởi mặt phẳng $(P)$ đi qua $I$ và song song với $A B,\, S C$.
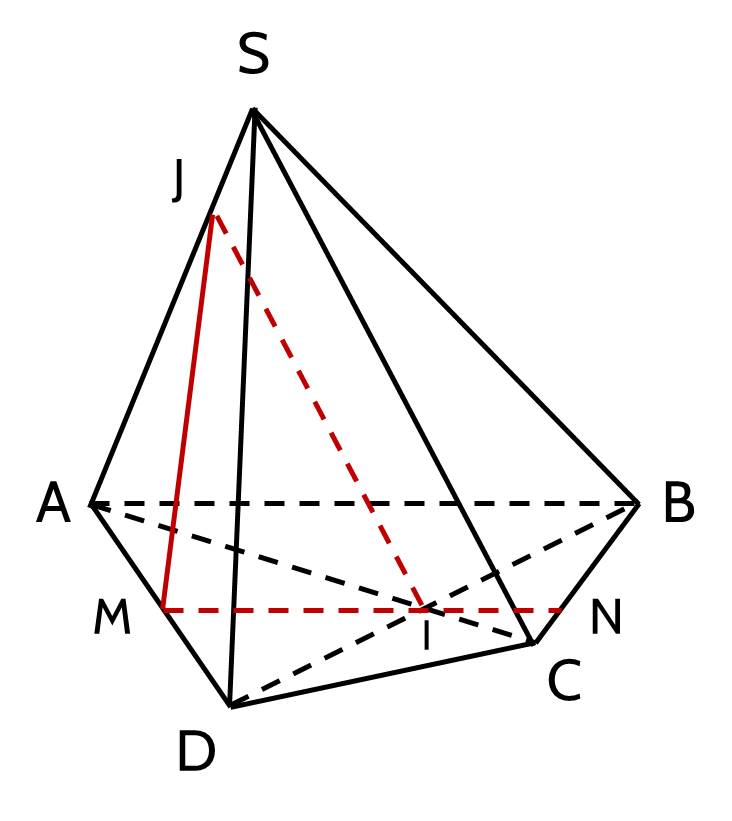
Giải
Ta dựng mặt phẳng $(P)$ như sau.
+ Trong mp $(SAC)$ dựng $IJ$ // $SC$ với $J \in SA.$
+ Trong mp $(ABCD)$ dựng $MN$ // $AB$ với $M \in AD$ và $N \in BC$.
Vậy $(MIJ) \equiv (P)$.
Ta có:
+ $(MIJ) \cap (SAD) =JM$
+ $(MIJ) \cap (ABCD) =MN$
Ta dựng giao tuyến của mặt phẳng $(MIJ)$ và $(SAB)$:
Điểm chung thứ nhất: $J$
Mặt khác $\left\{\begin{aligned}& MI // AB \\& MI \subset (MIJ) \\& AB \subset (SAB) \end{aligned}\right.$
$\Rightarrow$ giao tuyến của hai mặt phẳng $(MIJ)$ và $(SAB)$ là đường thẳng đi qua $J$ và song song với $AB$.

Vẽ $JP // AB$ với $P \in SB$.
Ta thấy:
+ $(MIJ) \cap (SAB) =JP$
+ $(MIJ) \cap (SBC) =NP$
Vậy thiết diện cần tìm là $MNPJ$.
Bạn có thể đăng câu hỏi về bài học này ở đây
