Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Mặt phẳng tọa độ và đồ thị hàm số SVIP
1. MẶT PHẲNG TỌA ĐỘ
MẶT PHẲNG TỌA ĐỘ
Trên mặt phẳng, ta vẽ hai trục số $Ox$, $Oy$ vuông góc với nhau và cắt nhau tại gốc $O$ của mỗi trục số như hình vẽ.
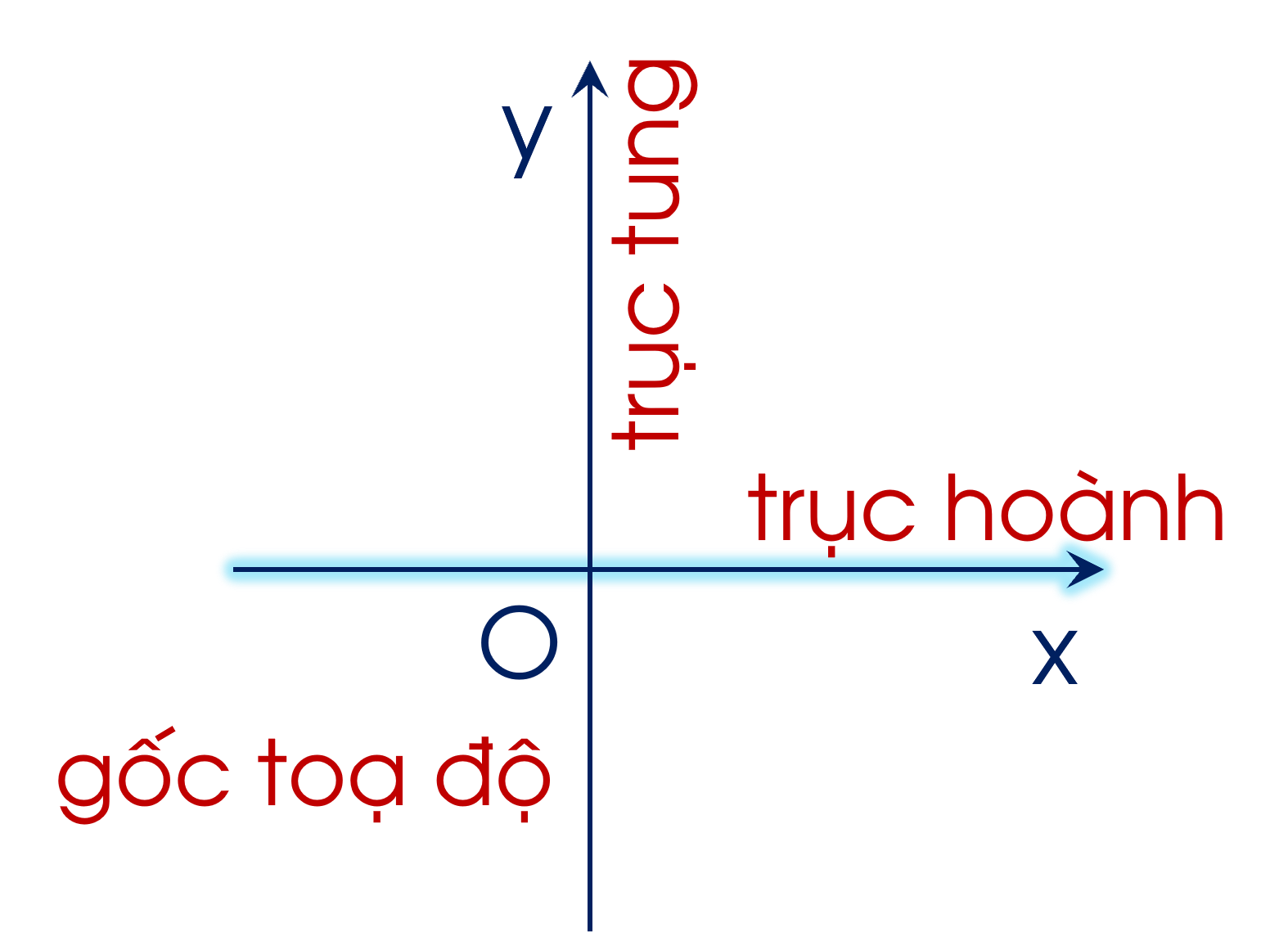
+ Các trục $Ox$ và $Oy$ gọi là các trục toạ độ, $Ox$ thường vẽ nằm ngang và gọi là trục hoành, $Oy$ thường vẽ thẳng đứng và gọi là trục tung;
+ Giao điểm $O$ gọi là gốc toạ độ.
$\rightarrow$ Mặt phẳng có hệ trục toạ độ $Oxy$ gọi là mặt phẳng toạ độ.
TỌA ĐỘ ĐIỂM TRONG MẶT PHẲNG TỌA ĐỘ
Trong mặt phẳng toạ độ, mỗi điểm $M$ xác định duy nhất một cặp số $(x_0 ; y_0)$ và mỗi cặp số $(x_0 ; y_0)$ xác định duy nhất một điểm $M$.
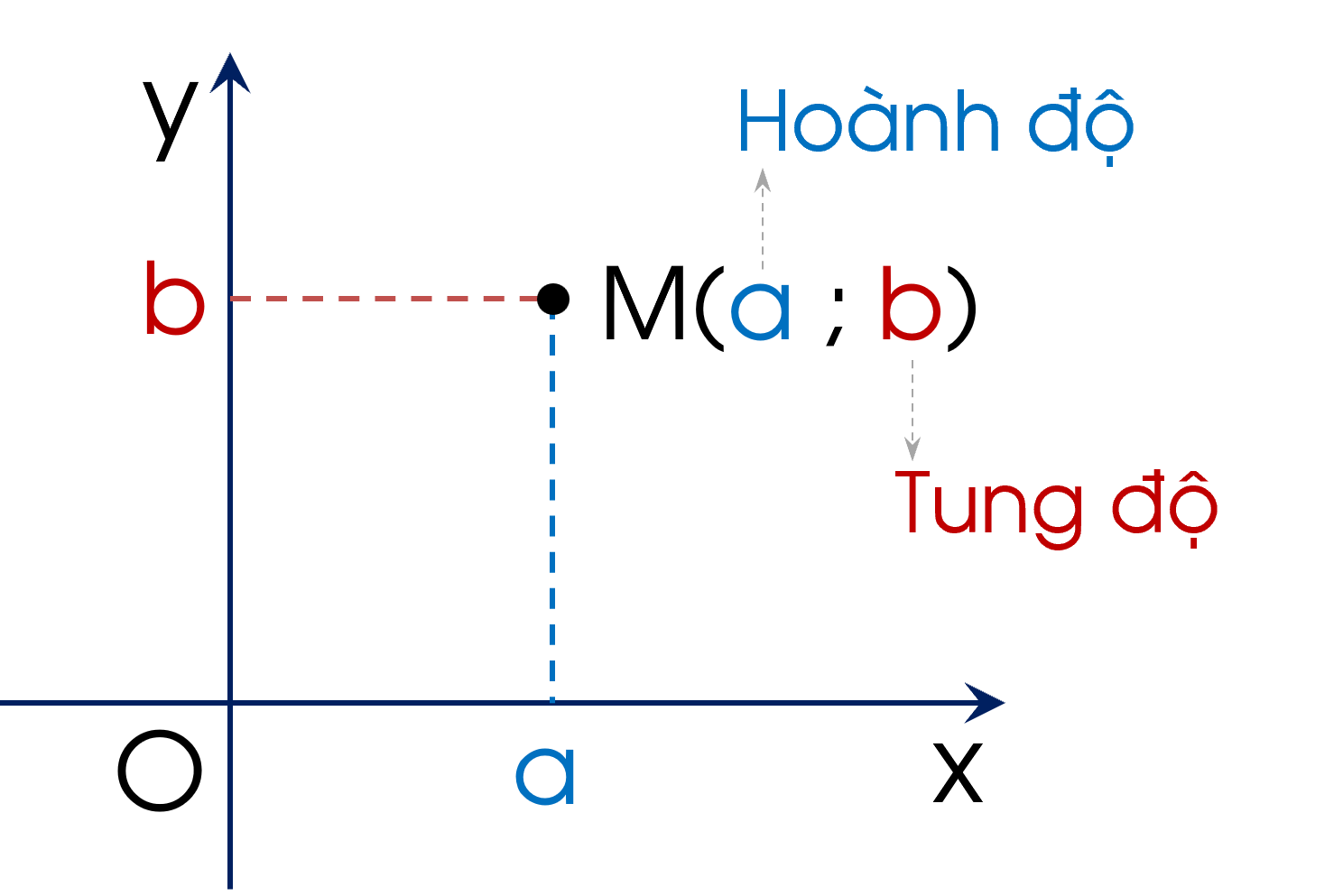
Cặp số $(x_0 ; y_0)$ là tọa độ điểm $M$; kí hiệu $M(x_0 ; y_0)$. Trong đó, $x_0$: hoành độ của điểm $M$; $y_0$: tung độ của điểm $M$.
CHÚ Ý
+ Hệ trục toạ độ $Oxy$ chia mặt phẳng toạ độ thành 4 góc phần tư (góc phần tư thứ I, II, III, IV).
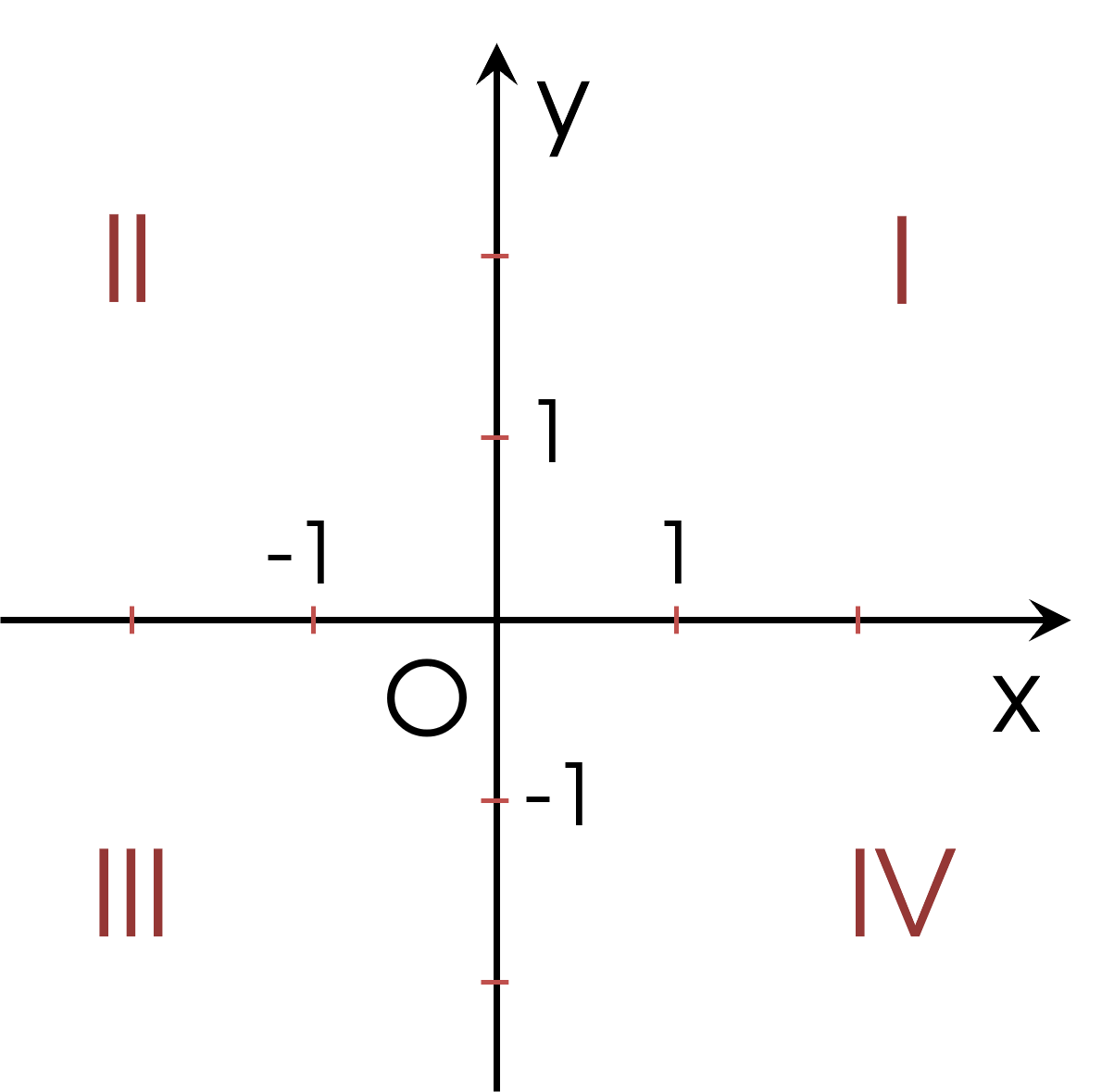
+ Các điểm có hoành độ (hoặc tung độ) bằng $0$ nằm trên trục tung $Oy$ (hoặc trục hoành $Ox$).
VÍ DỤ 1. $M(0 ; b)$ thuộc $Oy$; $N(a ; 0)$ thuộc $Ox$.
VÍ DỤ 2. Trong mặt phẳng tọa độ $Oxy$, xác định các điểm $R(2 ; -2)$.
Lời giải
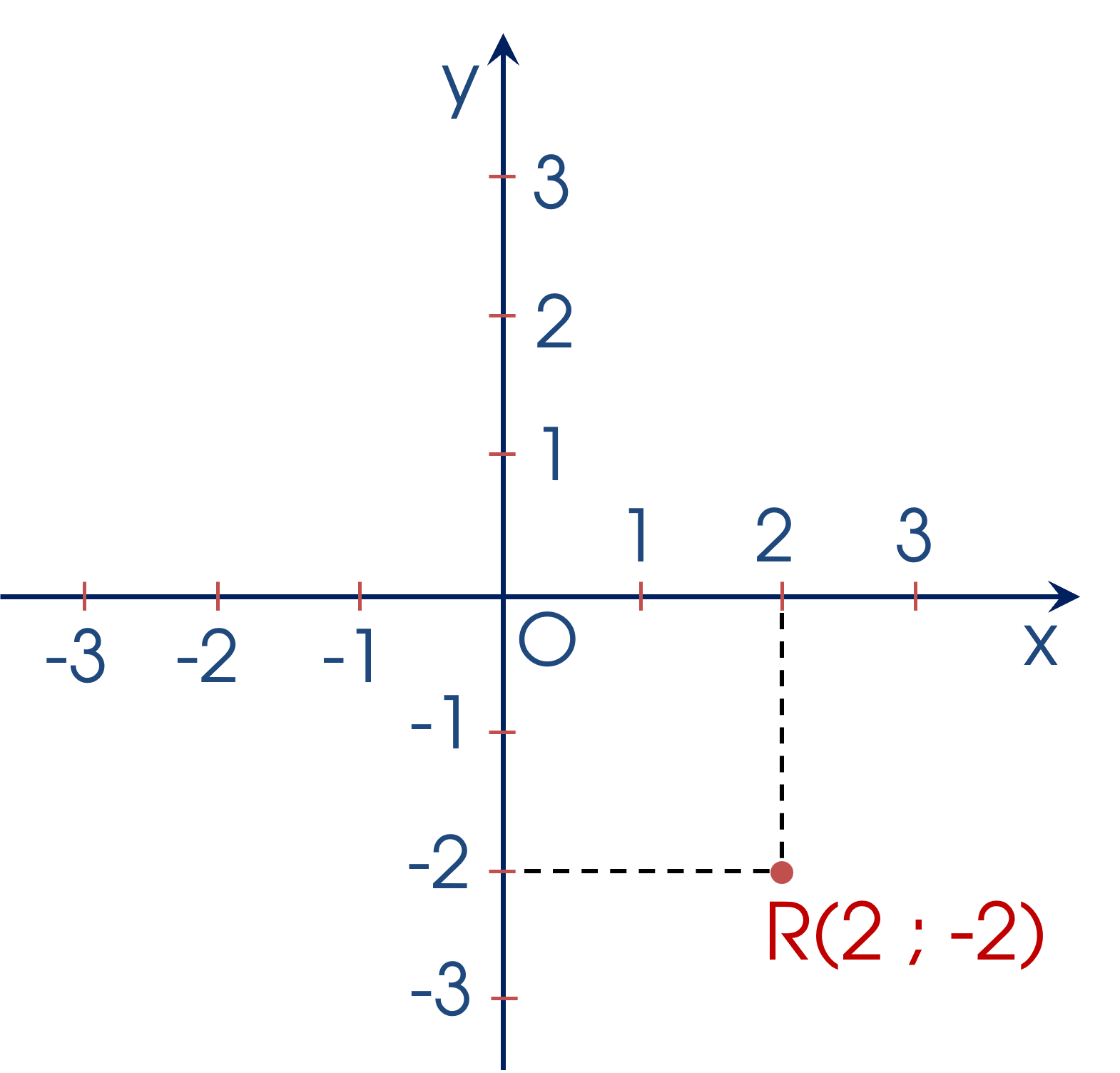
+ Qua điểm $2$ trên trục $Ox$, kẻ đường thẳng vuông góc với trục $Ox$;
+ Qua điểm $-2$ trên trục $Oy$, kẻ đường thẳng vuông góc với trục $Oy$.
+ Hai đường thẳng đó cắt nhau tại điểm $R(2 ; -2).$
2. ĐỒ THỊ HÀM SỐ
ĐỊNH NGHĨA
Đồ thị của hàm số $y = f(x)$ là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng $(x ; y)$ trên mặt phẳng toạ độ.
VÍ DỤ 3. Vẽ đồ thị của hàm số $y = f(x)$ cho bởi bảng:
| $x$ | $-2$ | $-1$ | $\dfrac32$ | $3$ |
| $y$ | $-\dfrac72$ | $-2$ | $2$ | $4$ |
Lời giải
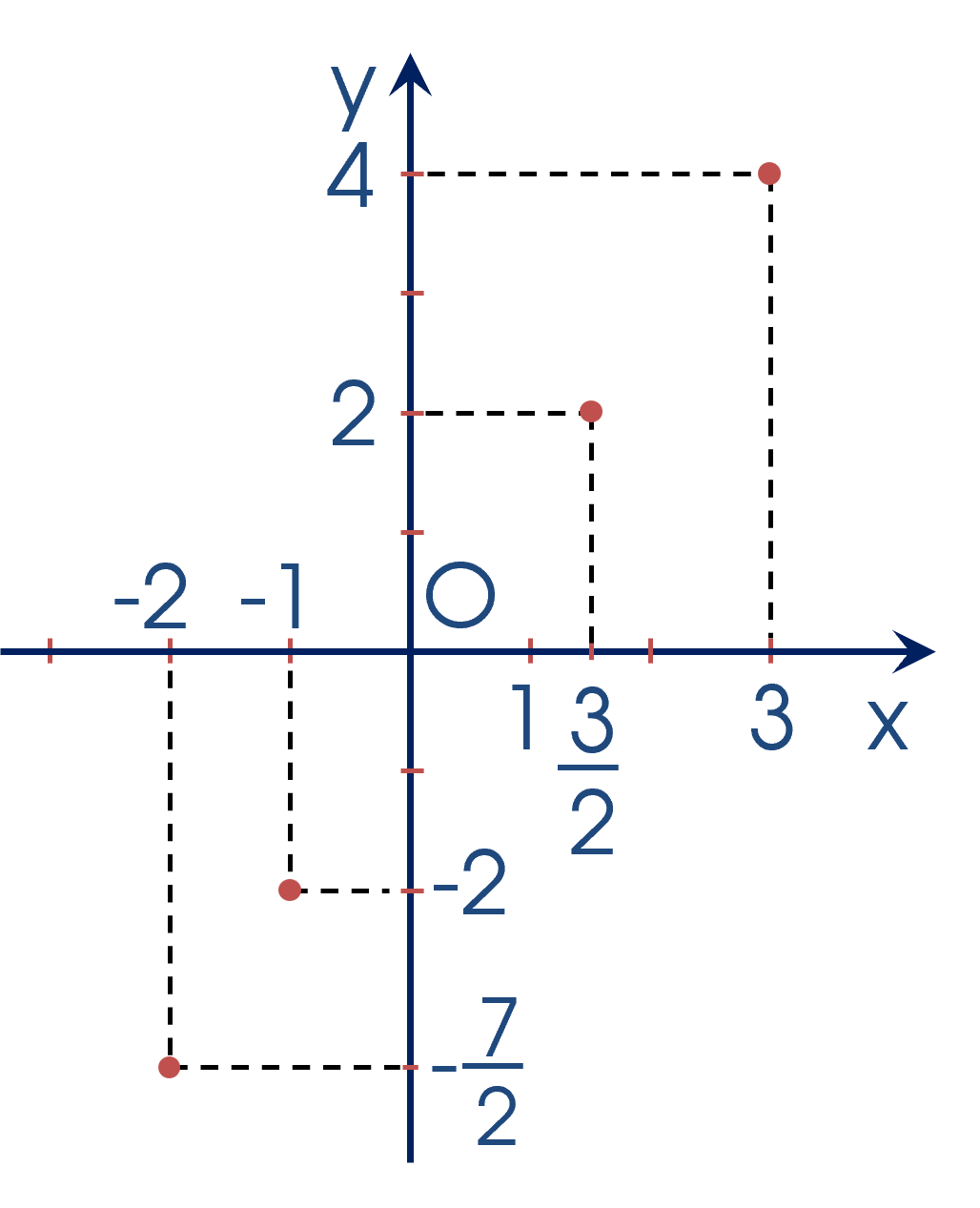
Đồ thị hàm số $y = f(x)$ gồm 4 điểm như hình vẽ trên.
VÍ DỤ 4. Trong mặt phẳng tọa độ $Oxy$, cho đồ thị của hàm số $y = x + 2$.
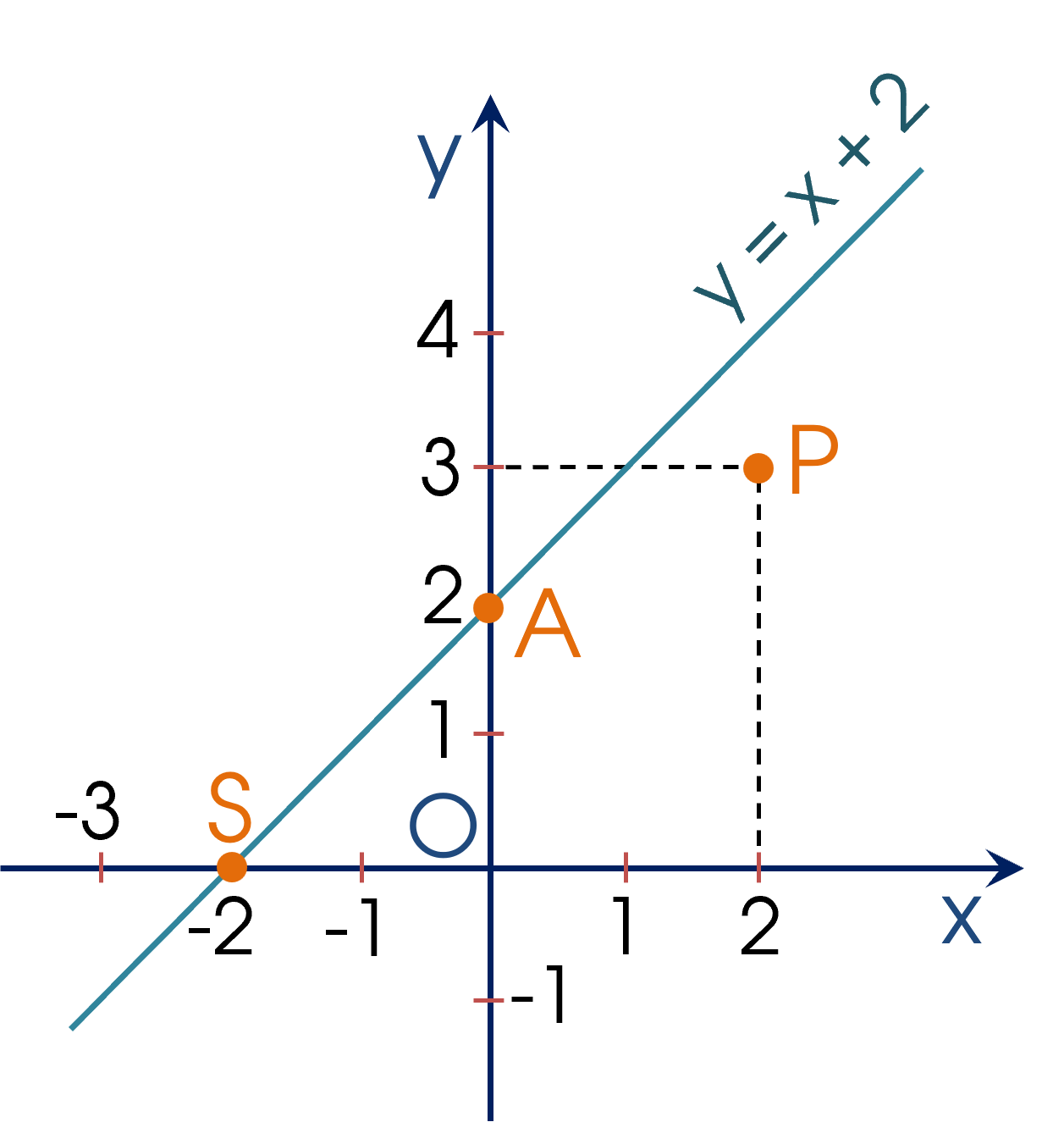
a) Điểm nào sau đây thuộc/ không thuộc đồ thị của hàm số?
$A(0;2)$; $S(-2;0)$ và $P(2;3)$
b) Điểm $D(2 \, 022 ; 2 \, 023)$ có thuộc đồ thị của hàm số hay không?
Lời giải
a) Quan sát đồ thị của hàm số $y = x + 2$, ta thấy:
+ $A(0 ; 2)$, $S(-2 ; 0)$ thuộc đồ thị của hàm số;
+ $P(2 ; 3)$ không thuộc đồ thị của hàm số.
b) Đối với hàm số $y = x + 2$, giá trị của $y$ tương ứng với giá trị $x = 2$ $022$ là:
$y = 2$ $022 + 2 = 2$ $024 \ne 2$ $023$
Vì vậy, điểm $D(2 022 ; 2 023)$ không thuộc đồ thị của hàm số.
Bạn có thể đăng câu hỏi về bài học này ở đây
