Bài học cùng chủ đề
- Lý thuyết
- Hàm số mũ
- Hàm số lôgarit
- Tập xác định của hàm số mũ, lôgarit
- Đạo hàm của hàm số mũ, logarit
- Sự biến thiên của hàm số mũ, logarit
- Đồ thị của hàm số mũ, lôgarit
- Tính giá trị một số biểu thức mũ, logarit
- Tìm Max, Min của biểu thức có chứa lôgarit
- Bài toán tăng trưởng, lãi suất
- Luyện tập tổng hợp
- Phiếu bài tập: Hàm số mũ - hàm số lôgarit
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lý thuyết SVIP
A. HÀM SỐ MŨ
1. Định nghĩa
Cho số thực dương $a$ khác $1$. Hàm số $y=a^x$ được gọi là hàm số mũ cơ số $a$.
2. Đạo hàm của hàm số mũ
+ Hàm số $y =e^x$ có đạo hàm tại mọi $x$
$(e^x)'=e^x$
+ Hàm số $y=a^x$, ($a>0, a\ne 1$) có đạo hàm tại mọi $x$
$(a^x)'=a^x. \ln a$
+ Chú ý: Đối với các hàm hợp $y=e^{u(x)}$ và $y=a^{u(x)}$, ta có:
$(e^u)'=u'. e^u$;
$(a^u)'=a^u. \ln a. u'$.
Ví dụ 1.
3. Khảo sát hàm số mũ
Xét hàm số $y=a^x$, $(a>0$, $a \ne 1)$
a. Tập xác định $D=\mathbb R$.
b. Sự biến thiên
- Chiều biến thiên:
+ $a>1$: hàm số luôn đồng biến;
+ $0<a<1$: hàm số luôn nghịch biến.
- Tiệm cận: trục $Ox$ là tiệm cận ngang.
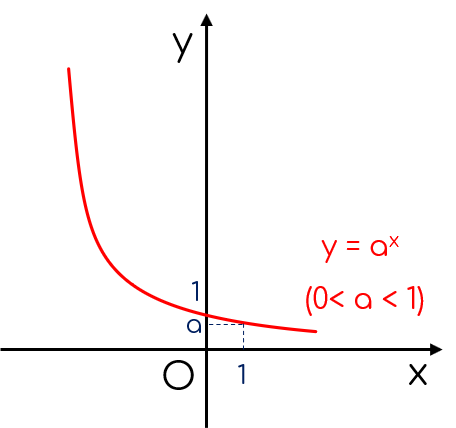
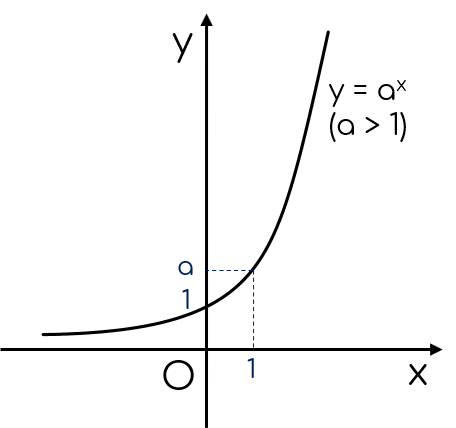
d. Đồ thị
+ Đi qua các điểm $(0;1)$, $(1;a)$;
+ Luôn nằm phía trên trục hoành vì $y=a^x>0, \forall x \in \mathbb R$.
+ Dạng đồ thị hàm số
|
|
|
B. HÀM SỐ LÔGARIT
1. Định nghĩa
Cho số thực dương $a$ khác 1. Hàm số $y=\log_a x$ được gọi là hàm số lôgarit cơ số $a$.
2. Đạo hàm của hàm số lôgarit
+ Hàm số $y=\log_a x$, $(a>0, a \ne 1)$ có đạo hàm tại mọi $x>0$
$(\log_a x)'= \dfrac1{x \ln a}$.
+ Đặc biệt: $(\ln x)'=\dfrac 1x$
+ Chú ý: Đối với hàm hợp $y= \log_a u(x)$ ta có: $(\log_au)'= \dfrac{u'}{u.\ln a}$.
3. Khảo sát hàm số lôgarit
Xét hàm số $y=\log_a x$, $ (a>0, a \ne 1)$
a. Tập xác định $D= (0; +\infty)$.
b. Sự biến thiên
- Chiều biến thiên:
+ $a>1$: hàm số luôn đồng biến;
+ $0<a<1$: hàm số luôn nghịch biến.
- Tiệm cận: trục $Oy$ là tiệm cận đứng.
d. Đồ thị
+ Đi qua các điểm $(1;0)$, $(a; 1)$;
+ Nằm phía bên phải trục tung.
+ Dạng đồ thị hàm số
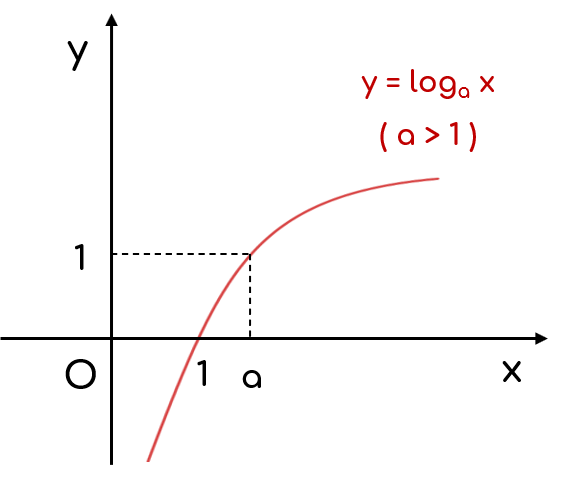 |
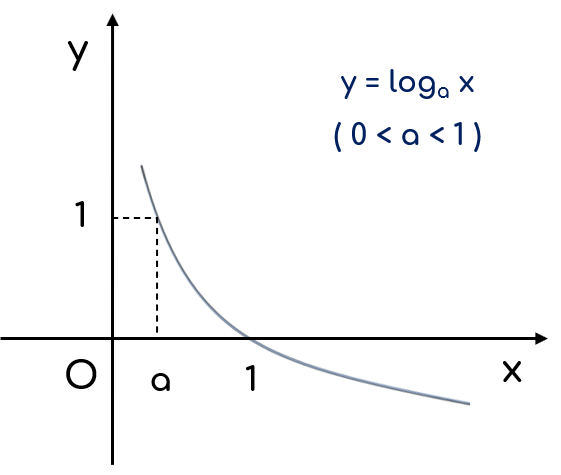 |
C. Liên hệ hàm số mũ và hàm số lũy thừa cùng cơ số
1. Nhận xét
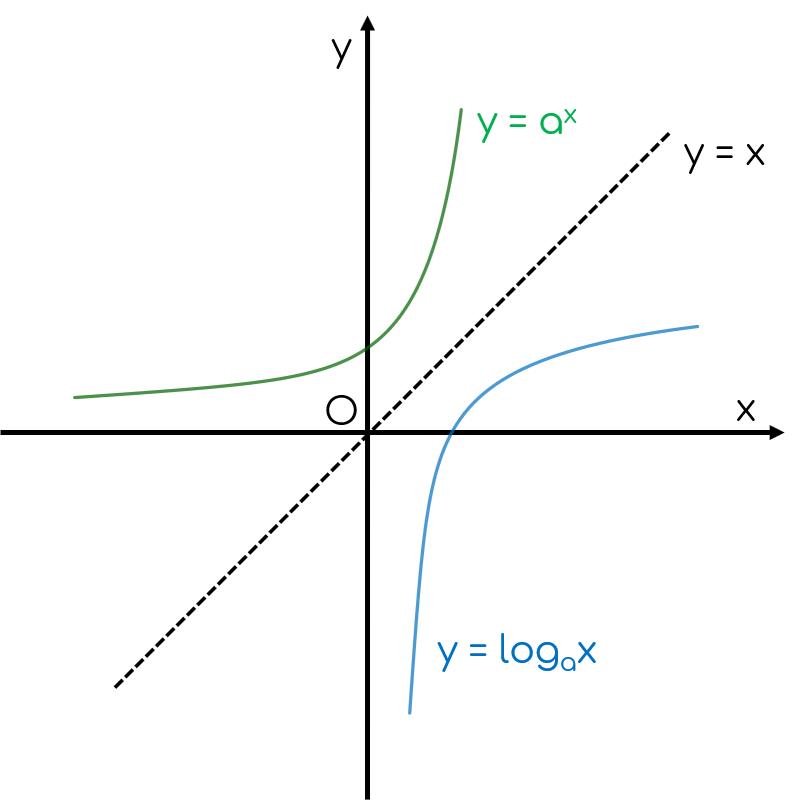
Đồ thị các hàm số $y=a^x$ và $y=\log_a x$, $(a>0, a \ne 1)$ đối xứng nhau qua đường thẳng $y=x$.
2. Đồ thị
 |
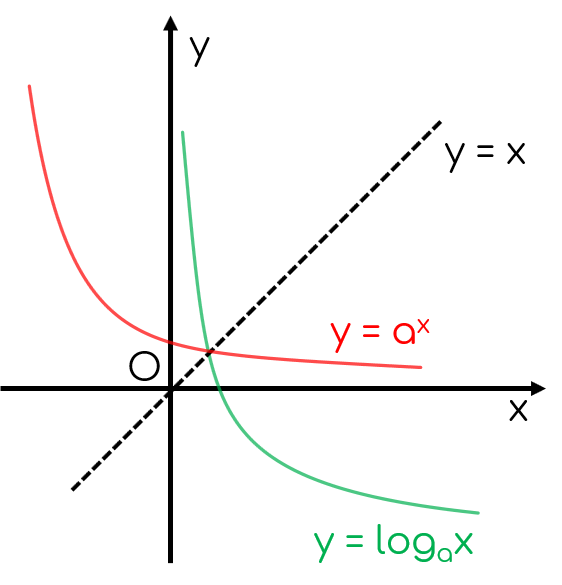 |
| $a>1$ | $0<a<1$ |
Bạn có thể đăng câu hỏi về bài học này ở đây