Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Lý thuyết SVIP
1. Các phép toán bit
a) Định nghĩa
Mọi dữ liệu trong máy tính đều có dạng dãy các bit.
Bốn phép toán bit cơ sở (hay phép toán logic với các bit) là NOT, AND, OR và XOR.
Phép toán NOT
NOT là phép toán có một toán hạng cho kết quả trái ngược với đầu vào.
Ví dụ: Toán hạng đầu vào là x. Bảng kết quả phép toán NOT như sau:
| x | NOT x |
| 0 | 1 |
| 1 | 0 |
Phép toán AND
Phép toán AND (hay phép nhân logic) có hai toán hạng cho kết quả là 1 khi và chỉ khi cả hai bit toán hạng đều là 1; bằng 0 trong những trường hợp còn lại.
Ví dụ: Hai toán hạng đầu vào là x, y. Bảng kết quả phép toán AND như sau:
| x | y | x AND y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Phép toán OR và XOR
Hai phép toán này đều có hai toán hạng.
Phép toán OR (hay phép cộng logic) cho kết quả là 0 khi và chỉ khi cả hai bit toán hạng đều là 0.
Phép toán XOR cho kết quả là 1 khi và chỉ khi hai bit toán hạng trái ngược nhau.
Ví dụ: Hai toán hạng đầu vào là x, y. Bảng kết quả phép toán OR và XOR như sau:
| x | y | x OR y | x XOR y |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 |
b) Các phép toán bit với dãy bit
Mỗi phần tử dữ liệu số hóa là một dãy bit liền nhau với độ dài ấn định trước.
Cách áp dụng bốn phép toán cơ sở cho các dãy bit như sau:
- Phép toán một toán hạng NOT (cũng gọi là phép bù) thực hiện với từng bit trong dãy. Phần bù của 0 là 1, của 1 là 0.
- Các phép toán hai toán hạng được thực hiện với từng cặp bit từ hai toán hạng dóng cột tương ứng với nhau. Các dãy bit có cùng độ dài.
Các ví dụ minh họa như sau:
- Phép toán một toán hạng:
| x | 10101011 |
| NOT x | 01010100 |
- Phép toán hai toán hạng:
| x | 10101011 |
| y | 10011001 |
| x AND y | 10001001 |
| x OR y | 10111011 |
| x XOR y | 00110010 |
2. Hệ nhị phân và ứng dụng
a) Hệ nhị phân
Cơ số trong một hệ đếm
Hệ nhị phân (hệ đếm cơ số 2) chỉ dùng hai kí số là 0 và 1, giá trị của kí số tăng gấp 2 lần khi dịch sang trái một vị trí cột.
Ví dụ minh họa: Chuyển đổi biểu diễn số 101101 (hệ nhị phân) sang thập phân như sau:
101101 \(\rightarrow\) 1 x 25 + 0 x 24 + 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = 45
b) Chuyển đổi một số nguyên dương ở hệ thập phân sang hệ nhị phân
Ví dụ chuyển đổi số 13 ở hệ thập phân sang nhị phân:
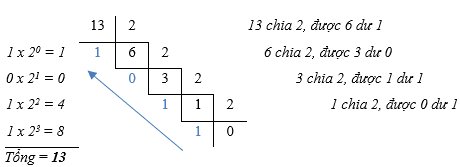
Lưu ý: Khi phần nguyên của kết quả là 0 thì kết thúc. Dãy các kí số 0 và 1 ghi lại phần dư các phép chia sẽ tạo thành số nhị phân cần tìm.
c) Phép cộng và pháp nhân hai số nguyên trong hệ nhị phân
Các phép toán trong hệ nhị phân đều thực hiện với hai dãy bit biểu diễn hai toán hạng và thực hiện tương tự như hệ thập phân.
Phép cộng
Bảng cộng cơ sở như sau:
| x | y | x + y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 10 |
Bảng cộng cơ sở giống với phép toán XOR nhưng trường hợp cả hai toán hạng đều bằng 1 thì kết quả là "viết 0 nhớ 1".
Ví dụ minh họa:
| x | 00111 |
| y | 10011 |
| x + y | 11010 |
Phép nhân
Bảng nhân cơ sở như sau:
| x | y | x * y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ví dụ minh họa: Từng bước làm phép tính nhân x = 100101 với y = 101 như sau:

d) Vai trò của hệ nhị phân trong tin học
Nhờ có hệ nhị phân mà máy tính có thể tính toán, xử lí thông tin định lượng tương tự như con người dùng hệ thập phân.
Hệ nhị phân đặt cơ sở cho sự ra đời của máy tính điện tử, là cơ sở cảu các thiết bị xử lí thông tin kĩ thuật số.
Bạn có thể đăng câu hỏi về bài học này ở đây
