Kiến thức nền tảng: Hệ thức lượng trong tam giác vuông SVIP

1. Tỉ số lượng giác của một góc nhọn

Cho góc nhọn $\alpha$.  Xét tam giác $ABC$ vuông tại $A$ có $\widehat{B} = \alpha$.

⚡Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc $\alpha$, kí hiệu $\sin \alpha$.

$\sin \alpha$ = cạnh đối : cạnh huyền

⚡Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc $\alpha$, kí hiệu $\cos \alpha$.

$\cos \alpha$ = cạnh kề : cạnh huyền

⚡Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc $\alpha$, kí hiệu $\tan \alpha$.

$\tan \alpha$ = cạnh đối : cạnh kề

⚡Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc $\alpha$, kí hiệu $\cot \alpha$.

$\cot \alpha$ = cạnh kề : cạnh đối

Ví dụ 1. Tính các tỉ số lượng giác của góc $B$ trong tam giác $ABC$.

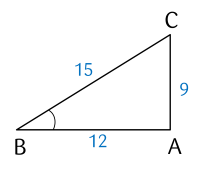
Lời giải

Xét tam giác $ABC$ có $\widehat{A} = 90^\circ$ và $B$ là góc nhọn.

$\sin B = \dfrac{AC}{BC} = \dfrac9{15} = 0,6$;

$\cos B = \dfrac{AB}{BC} = \dfrac{12}{15} = 0,8$;

$\tan B = \dfrac{AC}{AB} = \dfrac9{12} = 0,75$;

$\cot B = \dfrac{AB}{AC} = \dfrac43$.

Chú ý: Các tỉ số lượng giác của góc nhọn $a$ luôn dương, $\sin a < 1$; $\cos a < 1$ và $\cot a = \dfrac1{\tan a}$.

 2. Tỉ số lượng giác của góc nhọn đặc biệt

Ví dụ 2. Tính giá trị của biểu thức $P = \dfrac{\sin 30^\circ . \cos 60^\circ}{\tan 45^\circ}$.

Lời giải

$P = \dfrac{\sin 30^\circ . \cos 60^\circ}{\tan 45^\circ} = \dfrac{\dfrac12 . \dfrac12}1 = \dfrac14.$

3. Tỉ số lượng giác của hai góc phụ nhau

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Với $0^\circ < a < 90^\circ$ ta có:

⚡$\sin (90^\circ - a) = \cos a$;                    ⚡$\cos (90^\circ - a) = \sin a$;

⚡$\tan (90^\circ - a) = \cot a$;                    ⚡$\cot (90^\circ - a) = \tan a$;

4. Hệ thức giữa cạnh huyền và cạnh góc vuông

Định lí 1

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.

5. Hệ thức giữa hai cạnh góc vuông

Định lí 2

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

6. Giải tam giác vuông

Trong tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn, một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó. Ta gọi đó là việc giải tam giác vuông.

Ví dụ 3. Cho tam giác $ABC$ vuông tại $A$ có $AB = 3$, $B = 42^\circ$. Tính góc $C$ và các cạnh $AC$, $BC$ (làm tròn đến chữ số thập phân thứ ba)

Lời giải

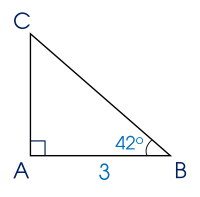
Tam giác $ABC$ vuông tại $A$.

Ta có $\widehat C = 90^\circ - \widehat B = 90^\circ - 42^\circ = 48^\circ$.

$AC = AB . \tan B = 3 . \tan 42^\circ \approx 2,701$.

Theo định nghĩa các tỉ số lượng giác:

$\cos B = \dfrac{AB}{BC} $ suy ra $BC = \dfrac{AB}{\cos B} = \dfrac3{\cos 42^\circ} \approx 4,037$.