Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Kiểm tra cuối chương I SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Hàm số y=2x3−6x−3 nghịch biến trên khoảng nào sau đây?
Hàm số nào sau đây đồng biến trên R?
Cho hàm số y=f(x) có đạo hàm f′(x)=x2(x2−1). Điểm cực tiểu của hàm số y=f(x) là
Hàm số y=−x4+2x2−3 có điểm cực đại xđ và điểm cực tiểu xt lần lượt là
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=x+x1 trên đoạn [23;3] lần lượt là
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x)=x+12x−1 trên đoạn [0;3]. Giá trị M−m bằng
Cho hàm số y=f(x) xác định và liên tục trên R có x→+∞limf(x)=5 và x→−∞limf(x)=−5. Khẳng định nào sau đây đúng?
Tiệm cận xiên của đồ thị hàm số y=f(x)=x+2+x−21 có phương trình là
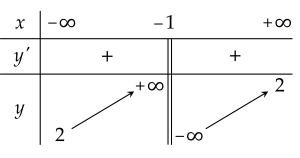
Hình trên là bảng biến thiên của hàm số nào trong bốn hàm số dưới đây?
Cho hàm số y=−x3+3x+2 có đồ thị là (C). Đồ thị (C) tiếp xúc với trục hoành tại điểm có hoành độ bằng bao nhiêu?
Hàm số y=x+1x2−x+2 nghịch biến trên khoảng nào sau đây?
Hàm số y=f(x) có đạo hàm y=f′(x) liên tục trên R và có đồ thị như hình dưới đây.
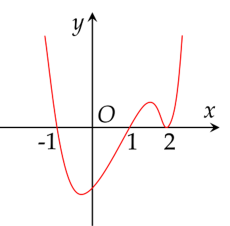
Số điểm cực đại của hàm số y=f(x) là
Có tất cả bao nhiêu giá trị khác nhau của tham số m để đồ thị hàm số y=x2+mx+4x−1 có hai đường tiệm cận?
Phương trình x3−1−x2=0 có bao nhiêu nghiệm thực phân biệt?
Cho hàm số y=x−1x2−2x−3.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đồ thị hàm số nhận đường thẳng y=x+1 làm tiệm cận xiên. |
|
| b) Hàm số có hai điểm cực trị. |
|
| c) Gọi A,B,C là giao điểm của đồ thị hàm số với các trục Ox,Oy. Diện tích tam giác ABC bằng 6. |
|
| d) Có đúng hai giá trị nguyên của tham số m để hàm số f(x)=x−1x2−2x−3−m2x đồng biến trên từng khoảng xác định. |
|
Cho hàm số f(x)=e2x−2x.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số có tập xác định là R. |
|
| b) Đạo hàm của hàm số đã cho là f′(x)=2e2x−2. |
|
| c) Tập nghiệm của bất phương trình f′(x)>0 là S=(0;+∞). |
|
| d) Hàm số đã cho có giá trị cực tiểu bằng 0. |
|
Cho hàm số y=x−12x+3 (C).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Đồ thị hàm số (C) nhận đường thẳng y=2 là tiệm cận ngang. |
|
| b) Đồ thị hàm số (C) nhận I(2;3) là tâm đối xứng. |
|
| c) Tiếp tuyến của (C)tại giao điểm của (C) với Oy có phương trình y=−5x−3 . |
|
| d) Tích khoảng cách từ một điểm bất kỳ trên (C) tới 2 đường tiệm cận của nó luôn bằng 3. |
|
Cho hàm số y=x+2x2+3x+3 có đồ thị (C) và A, B là hai điểm cực trị của (C).
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) y′=(x+2)2x2+4x+3. |
|
| b) A và B nằm ở hai phía của trục tung. |
|
| c) Đường thẳng ABcó phương trình là y=2x+1. |
|
| d) A và B đối xứng nhau qua đường thẳng Δ có phương trình là x+2y+4=0. |
|
Có bao nhiêu giá trị nguyên của m∈[−2025;2025] để đồ thị hàm số y=x2+2(m−1)x+m2−2x−1 có đúng hai đường tiệm cận đứng?
Trả lời:
Cho hàm số y=x4−2mx2+4m−4 (m là tham số thực). Giá trị của m bằng bao nhiêu để đồ thị hàm số đã cho có 3 điểm cực trị tạo thành tam giác có diện tích bằng 1?
Trả lời:
Cho hàm số y=f(x)=1+x−11. Bình phương khoảng cách từ điểm I(1;1) tới một tiếp tuyến bất kì của đồ thị hàm số đạt giá trị lớn nhất bằng bao nhiêu? (kết quả viết dưới dạng số thập phân và làm tròn đến hàng phần mười)
Trả lời:
Cho hàm số y=x3−3mx2+(2m2+1)x−mx−3. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−6;6] để đồ thị hàm số có 4 đường tiệm cận?
Trả lời:
Cho hàm số y=x4−mx2+2m−1 có đồ thị là (Cm). Tổng tất cả các giá trị của m để (Cm) có ba điểm cực trị cùng với gốc tọa độ tạo thành bốn đỉnh của một hình thoi bằng bao nhiêu?
Trả lời:
