Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Hình có trục đối xứng SVIP

Lưu ý: Ở điểm dừng, nếu không thấy nút nộp bài, bạn hãy kéo thanh trượt xuống dưới.
Bạn phải xem đến hết Video thì mới được lưu thời gian xem.
Để đảm bảo tốc độ truyền video, OLM lưu trữ video trên youtube. Do vậy phụ huynh tạm thời không chặn youtube để con có thể xem được bài giảng.
Nội dung này là Video có điểm dừng: Xem video kết hợp với trả lời câu hỏi.
Nếu câu hỏi nào bị trả lời sai, bạn sẽ phải trả lời lại dạng bài đó đến khi nào đúng mới qua được điểm dừng.
Bạn không được phép tua video qua một điểm dừng chưa hoàn thành.
Dữ liệu luyện tập chỉ được lưu khi bạn qua mỗi điểm dừng.
Những hình sau đây có hay không có trục đối xứng?


.png)
- Không
- Có
Hình nào sau đây có trục đối xứng?


Gấp đôi tờ giấy hình thoi theo đường nét đứt để hai phần chồng khít lên nhau. Hình nào sau đây minh họa đường nét đứt đó?
.png)
.png)

Gấp đôi tờ giấy hình thoi để hai phần chồng khít lên nhau.

Khi mở tờ giấy ra thì đường nếp gấp trùng với
Cho ba tờ giấy hình chữ nhật giống nhau. Gấp đôi mỗi tờ giấy theo đường màu trắng thì những tờ giấy nào có hai phần chồng khít lên nhau?



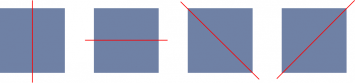
Gấp đôi 4 tờ giấy hình vuông theo các đường màu đỏ. Có bao nhiêu tờ giấy có hai phần chồng khít lên nhau?
Đường thẳng trong hình nào là trục đối xứng của tam giác đều đó?


Có bao nhiêu đường nét đứt trong hình vẽ sau là trục đối xứng của hình thoi?

Đáp số: đường.
Văn bản dưới đây là được tạo ra tự động từ nhận diện giọng nói trong video nên có thể có lỗi
- Xin chào mừng các em nó quay trở lại với
- khóa học Toán lớp 6 trên Trang onl.vn
- mày học năm nay thì chúng ta sẽ bắt đầu
- với một nội dung về hình học trong
- chương trình lớp 6 trước tiên các em hãy
- quan sát cho thấy một số các công trình
- kiến trúc ở cả 3 công trình kiến trúc
- này kem đều thấy được sự cân đối và hài
- hòa ở trong thiết kế và xây dựng nó tạo
- nên vẻ đẹp tính thẩm mỹ cho các công
- trình không chỉ xuất hiện ở trong xây
- dựng trong kiến trúc mà trong việc chụp
- ảnh để có một bức ảnh đẹp thì chúng ta
- cần có một bố cục và thông thưởng người
- ta sử dụng tính đối xứng để tạo ra những
- bức ảnh nghệ thuật như thế vợ chồng
- trước năm này thì chúng ta sẽ đi tìm
- hiểu về tính đối xứng của hình phẳng ở
- trong tự nhiên với đầu tiên với các hình
- có trục đối xứng trước khi tìm hiểu hình
- có trục đối xứng là gì thì các em quan
- sát vào cái hình sau đầu tiên với hai
- cánh bướm khi mà hai cánh bướm này
- sau khi cánh bướm sẽ gặp đôi theo đường
- lên đứt này chúng ta có hai phần phần
- cánh bên trái và phần cánh bên phải khi
- gặp Đô lại thì hai phần này sẽ chồng lên
- nhau tương tự như thế với đường tròn
- chúng ta gặp theo đường nét dứt đi qua
- tâm khi đó phần bên trên và phần dưới
- này cũng sẽ chồng khít lên nhau như vậy
- ở cả hai ngày này khi mà gặp đôi theo
- một đường Nhất định thì hai phần sẽ
- trồng ít về nhau khi đó chúng ta gọi
- Những hình này là những hình cố trục đối
- xứng trong thực tế sẽ còn rất nhiều
- những hình khác ví dụ như chiếc logo này
- biển báo giao thông cánh bướm 2 phòng
- thư các hình này đều có một đặc điểm
- chung có một đường thẳng d chia hình
- thành hai phần khi đổ nếu ta gấp các
- hình đó theo đường thẳng d thì hai phần
- sẽ chồng khít lên nhau các hình như thế
- ta gọi là hình có trục đối xứng
- A và đường thẳng d này người ta gọi là
- Trúc đối xứng của các hình đó ví dụ cài
- là quan sát ở mũi hình này mỗi đường
- thẳng d chia mỗi hình thành hai phần và
- nếu ta gấp hình đó theo đường thẳng d
- thì hai phần sẽ chồng khít lên nhau bốn
- hình ảnh này cũng là bốn ví dụ về hình
- có trục đối xứng ở trong thực tế ngoài
- ra kem vận dụng điều này và trả lời cho
- thầy có hỏi sau đây những hình nào sau
- đây sẽ có trục đối xứng trước khi xác
- định trục đối xứng và kiểm tra tính đối
- xứng của hình thì chúng ta sẽ quan sát
- xem những hình ảnh đó có 2 Hòa và cân
- đối 20 ở bốn hình ảnh này đều có một sự
- cân đối và hài hòa và nếu chúng ta gấp
- các hình đó theo các chụp mà kem đang
- quan sát ở đây mái đầu là qua đường
- thẳng đứng và hình ảnh cuối cùng là một
- đường chéo màu đỏ như thế này thì các
- đường thẳng đó chia mỗi hình thành hai
- phần khi gặp lại hai phần đó sẽ cho
- ở bên nhau rô đỏ cả bốn hình này đều là
- các hình có trục đối xứng và trên đây là
- các ví dụ về hình có trục đối xứng ở
- trong thực tế ngoài ra các em có thể kể
- ra rất nhiều những ví dụ khác về các
- hình có hoặc không có chủ đối xứng và ở
- trong Toán học thì chúng ta hãy cùng
- nhau đi tìm hiểu xem những hình phẳng
- nào sẽ có chủ đối xứng và không có chủ ý
- xứng Trước tiên với hình tròn thấy có
- một tờ giấy hình tròn với một tâm ở giữa
- như thế này các em gấp đôi tờ giấy sao
- cho hai phần sẽ chồng khít lên nhau ví
- dụ thầy sẽ gấp đôi tờ giấy như thế này
- sau đó chúng ta sẽ mở tờ giấy ra và kèm
- quan sát được một nét gấp mà thấy minh
- họa bằng đường nét dứt ở đây đường nét
- đứt này chính là trục đối xứng của hình
- tròn bởi vì lương Thằng đó chia hình
- tròn thành hai phần và khi ta gấp lại
- hai phần đó chồng khít lên nhau khi đó
- đường thẳng
- Đó là một chút đối xứng của hình tròn và
- chúng ta có rất nhiều đường thẳng đi qua
- tâm của hình tròn do đó tổng quan lên là
- mỗi đường thẳng đi qua tâm đều là một
- trục đối xứng của hình tròn đó tương tự
- như vậy kem kiểm tra xem cho thầy chúng
- ta có những cách nào để gấp đôi tờ giấy
- hình thoi sao cho hai thằng chồng khít
- lên nhau sâu đỏ chúng ta sẽ mở tờ giấy
- ra và kèm quan sát được một nét gấp mà
- thấy minh họa bằng đường nét dứt ở đây
- các em nhận xét cho thầy lên cấp độ 2 có
- đặc điểm gì so với từ giấy hình thoi mà
- chúng ta có bán đâu đường nét đứt này
- cũng trùng với đường chéo của hình thoi
- và ta có một cái luận đường chéo của
- hình thoi là một trục đối xứng của hình
- thoi đó với các em kiểm tra xem đường
- chéo còn lại của hình thoi có phải là
- trục đối xứng của hình thoi này không
- nhất chính xác như vậy tổng
- đi tìm mỗi đường chéo sẽ là một trục đối
- xứng của hình thoi đã cho đó là hình
- tròn vàng thoi tiếp theo với hình chữ
- nhật với 3 tờ giấy hình chữ nhật giống
- hệt nhau như thế này với ba đường màu
- trắng kèm quan sát được ở đây chia mỗi
- tờ giấy thành 2 phần nếu ta gấp tờ giấy
- theo các đường màu trắng đó thì tờ giấy
- thứ nhất tờ giấy Thứ hai hai tờ giấy Thứ
- 3 sẽ có 2 phần chồng khít lên nhau chị
- có tờ giấy thứ nhất và tờ giấy thứ 2 sẽ
- có 2 phần chồng khít lên nhau con từ
- giới thứ ba thì hai phần gấp lại sẽ như
- thế này trúng không trùng khít với nhau
- Do đó hai đường thẳng này chính là các
- trục đối xứng của hình chữ nhật và đặc
- điểm chung của hai đường này thì đó đều
- là các đường thẳng đi qua trung điểm hai
- cạnh đối diện như vậy mỗi đường thẳng đi
- qua
- ở hai cạnh đối diện là một trục đối xứng
- của hình chữ nhật và trên đây là trục
- đối xứng của hình tròn hình thoi và hình
- chữ nhật tương tự như các hình này các
- em cũng có thể xét cho cái hình khoảng
- khác ví dụ thầy có câu hỏi sau đây kinh
- trục đối xứng của các hình hình vuông
- tam giác đều và đoạn thẳng AB đầu tiên
- là với hình vuông thì thấy cổ bốn hình
- vuông giống nhau như thế này tương ứng
- với mỗi hình là 4 đường màu vàng bún
- đường này chia mỗi hình vuông thành hai
- phần và nếu gấp hình vuông theo đường
- thẳng đó thì hai phần của hình vuông có
- trùng khít lên nhau hay không khi đó hai
- phần của mỗi hình vuông sẽ trùng khít
- lên nhau bún đường thẳng này cũng chính
- là Bốn trục đối xứng của hình vuông hình
- vuông có Bốn trục đối xứng các em đang
- quan sát được ở đây tương tự như thế với
- ăn kem cho thời tiết một trục đối xứng
- của tam giác đều sẽ là đường thẳng nào
- trong hai đường thẳng song đây nhất mỗi
- 2000 này thì chị có hình ảnh đầu tiên là
- đường thẳng chứa tam giác đều thành hai
- phần khi gặp đôi lại hai phần gỗ chồng
- khi về nhau con hình thứ 2 thì hai phần
- gặp lại sẽ không trùng khít da đỏ những
- đường thẳng mà đi qua đỉnh và vuông góc
- với cạnh đối diện của tam giác đều sẽ là
- trục đối xứng của tam giác đều mà tam
- giác đều thì có ba đình với các em có
- thể dự đoán mỗi tam giác đều sẽ có bao
- nhiêu trục đối xứng chúng ta sẽ cổ 3
- trục đối xứng cho các tam giác đều con
- với đoạn thẳng khi mà gấp đôi đoạn thẳng
- này điểm A trùng khít và điểm B Khi mà
- trục đối xứng đó sẽ đi qua trung điểm
- của AB và vuông góc với AB do đó đoạn
- thẳng của chúng ta sẽ cổ mua trục đối
- xứng chỉ vậy một hình có
- Em có hay hoặc là cố nhiều đối xứng phá
- tác đi tới một nhận xét một hình có thể
- có nhiều trục đối xứng Ví dụ như hình
- vuông là Bốn trục đối xứng tam giác đều
- là ba trục đối xứng đoạn thẳng là một
- chủ đối xứng nhận xét này cũng kết thúc
- cho nội dung bài học của chúng ta cây
- Cảm ơn sự theo dõi của kem và hẹn gặp
- lại các em trong các bài học tiếp theo
- trên org.vn
Bạn có thể đăng câu hỏi về bài học này ở đây
