olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Thông tin của bạn

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập xác định SVIP

Câu 1 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên như sau:

Khẳng định nào sau đây đúng?

max⁡[−3;2]f(x)=3\underset{[-3;2]}{\mathop{\max}} f(x)=3.
max⁡[−3;2]f(x)=−2\underset{[-3;2]}{\mathop{\max}} f(x)=-2.
max⁡[−3;2]f(x)=2\underset{[-3;2]}{\mathop{\max}} f(x)=2.
max⁡[−3;2]f(x)=1\underset{[-3;2]}{\mathop{\max}} f(x)=1.
Câu 2 (1đ):

Cho hàm số y=f(x)y=f(x) xác định, liên tục trên R\mathbb{R} và có bảng biến thiên sau:

Khẳng định nào sau đây đúng?

Giá trị nhỏ nhất của hàm số bằng −1.-1.
Giá trị lớn nhất của hàm số bằng 22.
Giá trị nhỏ nhất của hàm số bằng −1-1 và 11.
Giá trị nhỏ nhất của hàm số bằng 11.
Câu 3 (1đ):

Cho hàm số y=f(x)y=f(x) có bảng biến thiên như hình vẽ:

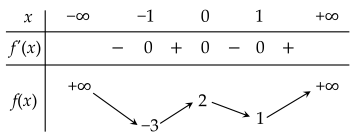
loading...

Giá trị nhỏ nhất của hàm số y=f(x)y = f(x) trên đoạn [−1;2][-1;2] là

00.
−3-3.
11.
22.
Câu 4 (1đ):

Cho hàm số bậc ba y=f(x)y=f(x) có đồ thị như hình vẽ:

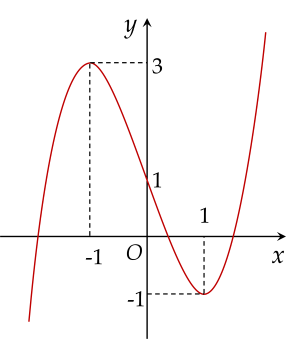
loading...

Trên đoạn [0;1][0;1], hàm số y=f(x)y = f(x) đạt giá trị nhỏ nhất tại

x=0x=0.
x=2x=2.
x=−1x=-1.
x=1x=1.
Câu 5 (1đ):

Cho hàm số y=f(x)y=f(x) liên tục trên đoạn [−1;3][-1;3] và có đồ thị như hình vẽ.

Cho hàm số $y=f(x)$ liên tục trên đoạn $[-1;3]$ và có đồ thị như hình vẽ

Giá trị lớn nhất của hàm số đã cho trên đoạn [−1;3][-1;3] bằng

11.
00.
33.
22.
Câu 6 (1đ):

Cho hàm số y=f(x)y=f(x) có đồ thị như hình vẽ dưới.

Giá trị lớn nhất của hàm số trên $[ -3;4 ]$ bằng

Giá trị lớn nhất của hàm số trên [−3;4][ -3;4 ] bằng

f(−3)f(-3).
f(4)f(4).
f(0)f(0).
f(2)f(2).
Câu 7 (1đ):

Cho hàm số y=f(x)y=f(x) có đồ thị trên đoạn [−1;1][-1;1] là đường cong như hình vẽ.

Cho hàm số $y=f(x)$ có đồ thị trên đoạn $[-1;1]$

Gọi M, mM, \, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x)f(x) trên đoạn [−1;1][-1;1]. Khi đó biểu thức M−mM-m bằng

22.
44.
33.
00.
Câu 8 (1đ):

Cho hàm số y=f(x)y=f\left( x \right) có bảng xét dấu đạo hàm như sau.

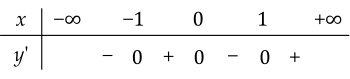
loading...

Mệnh đề nào sau đây đúng?

min⁡(−1; +∞) f(x)=f(0)\underset{\left( -1;\,+\infty \right)}{\mathop{\min }}\,f\left( x \right)=f\left( 0 \right).
max⁡(0; +∞) f(x)=f(1)\underset{\left( 0;\,+\infty \right)}{\mathop{\max}}\,f\left( x \right)=f\left( 1 \right).
min⁡(−∞; −1) f(x)=f(−1)\underset{\left( -\infty ;\,-1 \right)}{\mathop{\min }}\,f\left( x \right)=f\left( -1 \right).
max⁡(−1; 1] f(x)=f(0)\underset{\left( -1;\,1 \right]}{\mathop{\max}}\,f\left( x \right)=f\left( 0 \right).
Câu 9 (1đ):

Cho hàm số y=f(x)y=f(x) xác định và liên tục trên khoảng (−∞;12)\Big( -\infty ;\dfrac{1}{2} \Big) và (12;+∞)\Big(\dfrac{1}{2};+\infty\Big). Đồ thị hàm số y=f(x)y = f(x) là đường cong trong hình vẽ.

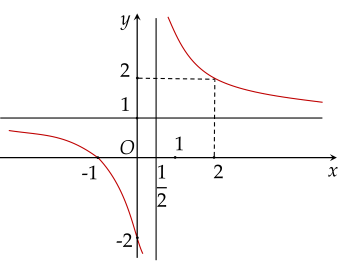
loading...

Khẳng định nào sau đây đúng?

max⁡[−2;1] f(x)=0\underset{\left[ -2;1 \right]}{\mathop{\max }}\,f\left( x \right)=0.
max⁡[1;2] f(x)=2\underset{\left[ 1;2 \right]}{\mathop{\max }}\,f\left( x \right)=2.
max⁡[3;4] f(x)=f(4)\underset{\left[ 3;4 \right]}{\mathop{\max }}\,f\left( x \right)=f\left( 4 \right).
max⁡[−3;0] f(x)=f(−3)\underset{\left[ -3;0 \right]}{\mathop{\max }}\,f\left( x \right)=f\left( -3 \right).
Câu 10 (1đ):

Cho hàm số y=f(x)y=f(x) liên tục trên R\mathbb{R} và có bảng biến thiên như hình dưới đây:

Khi đó giá trị nhỏ nhất của hàm số y=f(x)y=f(x) trên đoạn [−10;10][-10;10] bằng

143\dfrac{14}{3}.
112\dfrac{11}{2}.
−38-38.
−2-2.
Câu 11 (1đ):

Cho hàm số y=f(x)y=f(x) có đồ thị của đạo hàm y=f′(x)y=f'(x) như hình vẽ.

Giá trị lớn nhất của hàm số f(x)f(x) trên đoạn [−1;4][-1;4] bằng

f(0)f(0).
f(4)f(4).
f(1)f(1).
f(−1)f(-1).
Câu 12 (1đ):

Cho hàm số y=f(x)y = f\left( x \right) xác định, liên tục trên R\mathbb{R} và có bảng biến thiên như sau.

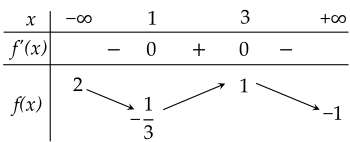
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số có giá trị cực đại bằng 33.
b) Hàm số có hai điểm cực trị.
c) Hàm số có giá trị lớn nhất bằng 11, nhỏ nhất bằng −13-\dfrac{1}{3}.
d) Đồ thị hàm số không cắt trục hoành.
Câu 13 (1đ):

Cho hàm số y=f(x)y=f(x) liên tục và có đồ thị trên đoạn [−2;4][-2 ; 4] như hình vẽ.

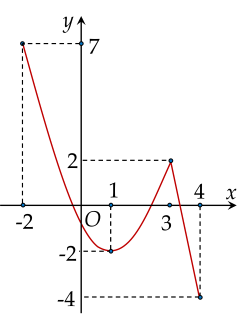
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Trên đoạn [−2;4][-2 ; 4], đồ thị hàm số y=f(x)y = f(x) có 22 điểm cực trị.
b) Giá trị nhỏ nhất của hàm số y=f(x)y = f(x) trên đoạn [−2;2][-2;2] là −2-2.
c) Giá trị lớn nhất của hàm số y=f(x)y = f(x) trên đoạn [1;4][1;4] là −4-4.
d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x)y = f(x) trên đoạn [−2;4][-2;4] là 1111.
Câu 14 (1đ):

Cho hàm số y=f(x)y=f(x) liên tục trên đoạn [−1;3][-1;3] và có đồ thị như hình vẽ.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số y=f(x)y=f(x) nghịch biến trên khoảng (0;2)(0;2).
b) max⁡[0;2]f(x)=1.\underset{[0;2]}{\mathop{\max}}f(x)=1.
c) Gọi M,mM,m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn [−1;3][-1;3]. Giá trị của M+mM+m là 22.
d) Xét hàm số g(x)=f(x+1)g(x)=f(x+1) thì max⁡[0;2]g(x)=−3.\underset{[0;2]}{\mathop{\max}}g(x)=-3.
25%
Đang tải dữ liệu câu hỏi
Hôm nay, bạn còn lượt làm bài tập miễn phí. Hãy đăng nhập hoặc đăng ký và xác thực tài khoản để trải nghiệm học không giới hạn!
OLM©2022OLM \copyright 2022
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP