Bài học cùng chủ đề
- Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Độ dài của cung tròn
- Hình quạt tròn và diện tích
- Hình vành khuyên và diện tích
- Độ dài đường tròn, cung tròn
- Diện tích hình tròn, hình quạt tròn
- Diện tích hình vành khăn, hình viên phân
- Phiếu bài tập tuần: Độ dài cung tròn. Diện tích hình quạt tròn, hình vành khuyên
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên SVIP
1. Độ dài của cung tròn
Độ dài cung $n^\circ$ của đường tròn bán kính $R$ là: $l = \dfrac{\pi Rn}{180}$
Ví dụ 1. Tính độ dài cung $30^\circ$ của một đường tròn có bán kính $10$ cm. (Lấy $\pi = 3,14$ và làm tròn kết quả đến hàng phần trăm)
Lời giải

Cung $30^\circ$, bán kính $R = 10$ cm có độ dài:
$l = \dfrac{\pi Rn}{180} = \dfrac{3,14 . 10 . 30}{180} \approx 5,23$ cm.
2. Hình quạt tròn
a. Định nghĩa
Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó.
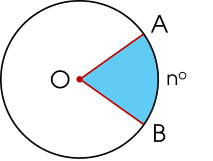
Ví dụ 2. Ta có hình quạt tròn AOB, tâm O, bán kính R, cung ứng với hình quạt có số đo $n^\circ$ (số đo $n^\circ$ được hiểu là số đo cung AB giới hạn hình quạt tròn đó).
Chú ý
+ Hình quạt tròn giới hạn bởi hai bán kính OA, OB và cung tròn AmB được gọi là hình quạt tròn OAmB hoặc hình quạt tròn OAB.
+ Người ta chứng minh được diện tích hình quạt tròn tỉ lệ thuận với số đo của cung ứng với nó.
b. Công thức diện tích
Diện tích $S_q$ của hình quạt tròn bán kính $R$ ứng với cung $n^\circ$:
$S_q = \dfrac n{360}\pi R^2 = \dfrac{lR}2$
Ví dụ 3. Tính diện tích của hình quạt tròn bán kính $5$ cm và có độ dài cung tương ứng với nó bằng $4\pi$ cm.
Lời giải
$S_q = \dfrac{lR}2 = \dfrac{4\pi.5}2 = 10\pi$ (cm$^2$)
3. Hình vành khuyên
a. Định nghĩa
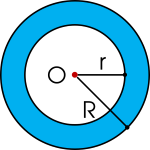
Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm).
b. Công thức diện tích
Diện tích $S_{vk}$ của hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là $R_1$ ; $R_2$ là:
$S_{vk} = \pi. (R_1^2 - R_2^2)$ với $R_1 > R_2$.
Ví dụ 4. Tính diện tích của hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là $3$ m và $5$ m.
Lời giải
$S_{vk} = \pi. (5^2 - 3^2) = 16\pi$ (cm$^2$)
Bạn có thể đăng câu hỏi về bài học này ở đây
