Bài học cùng chủ đề
- Giá trị lượng giác của một góc từ 0 độ đến 180 độ
- Giá trị lượng giác của một góc từ 0° đến 180°
- Quan hệ giữa các giá trị lượng giác của 2 góc bù nhau
- Định lí côsin
- Định lí sin
- Tính giá trị lượng giác của một góc bất kì từ 0° đến 180°
- Quan hệ của GTLG của hai góc bù nhau, phụ nhau
- So sánh các GTLG. Tính giá trị biểu thức lượng giác
- Luyện tập tổng hợp và GTLG một góc từ 0° đến 180°
- Định lí côsin, định lí sin và ứng dụng
- Bài tập tự luận (nâng cao)
- Phiếu bài tập: Giá trị lượng giác của một góc
- Phiếu bài tập: Định lí sin - côsin
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Định lí côsin, định lí sin và ứng dụng SVIP
Cho tam giác ABC có BC=a,CA=b,AB=c.
Điền kí hiệu thích hợp vào ô trống.
=b2+a2−2bacosC;
=c2+a2−2cacosB;
=2cbc2+b2−a2.
(Kéo thả hoặc click vào để điền)
Cho tam giác ABC có AB=11,BC=6,CA=7. Giá trị của cosA là
Cho tam giác ABC có AB=22,BC=22,CA=4. Số đo góc A bằng
Cho tam giác ABC có AB=16,CA=21,A=60∘. Độ dài cạnh BC là
Tam giác ABC có B=60∘,C=45∘ và AB=11. Độ dài cạnh AC là
Tam giác ABC có AB=3,AC=6 và A=60∘. Bán kính của đường tròn ngoại tiếp tam giác ABC là
Tam giác ABC vuông tại A có đường cao AH=512 cm và ACAB=43. Bán kính của đường tròn ngoại tiếp tam giác ABC là
Tam giác ABC có AB=2, AC=3 và C=45∘. Độ dài cạnh BC với BC>1 bằng
Cho hình thoi ABCD cạnh bằng 1 cm và có BAD=60∘. Độ dài cạnh AC bằng
Tam giác ABC có AB=26−2, BC=3, CA=2. Gọi D là chân đường phân giác trong góc A, góc ADB có số đo bằng
Cho góc xOy có số đo 30∘. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB=1. Độ dài lớn nhất của đoạn OB bằng
Cho góc xOy=30∘. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB=1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng
Tam giác ABC có AB=c, BC=a, CA=b. Các cạnh a, b, c liên hệ với nhau bởi đẳng thức b(b2−a2)=c(a2−c2). Khi đó góc BAC bằng
Tam giác nhọn ABC có AC=b,BC=a, BB′ là đường cao kẻ từ B và CBB′=α. Bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a,b và α là
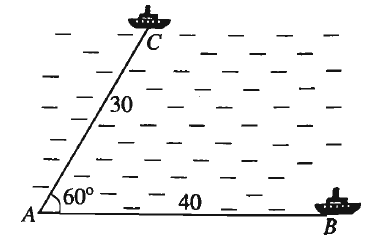
Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 60∘. Tàu B chạy với tốc độ 20 hải lý một giờ. Tàu C chạy với tốc độ 15 hải lý một giờ. Sau hai giờ, khoảng cách giữa hai tầu gần nhất với số nào sau đây?

Bạn có thể đăng câu hỏi về bài học này ở đây
