Đề số 3 SVIP

Hướng dẫn giải:

1) Thay $x = 9$ (thỏa mãn điều kiện) vào biểu thức $Q$ ta có:

$Q = \dfrac{\sqrt{9} + 3}{\sqrt{9} + 1} = \dfrac{3 + 3}{3 + 1} = \dfrac{6}{4} = \dfrac{3}{2}$

Vậy với $x = 9$ thì $Q = \dfrac{3}{2}$.

2) Với $x \geq 0; \, x \neq 1$ ta có:

$P = \dfrac{1}{\sqrt{x} + 2} - \dfrac{\sqrt{x}}{1 - \sqrt{x}} - \dfrac{3\sqrt{x}}{\sqrt{x} + 2}$

$= \dfrac{\sqrt{x} - 1 + \sqrt{x} (\sqrt{x} + 2) - 3\sqrt{x}}{(\sqrt{x} - 1)(\sqrt{x} + 2)}$

$= \dfrac{\sqrt{x} - 1 + x + 2\sqrt{x} - 3\sqrt{x}}{(\sqrt{x} - 1)(\sqrt{x} + 2)}$

$= \dfrac{x - 1}{(\sqrt{x} - 1)(\sqrt{x} + 2)}$ $= \dfrac{(\sqrt{x} - 1)(\sqrt{x} + 1)}{(\sqrt{x} - 1)(\sqrt{x} + 2)}$ $= \dfrac{\sqrt{x} + 1}{\sqrt{x} + 2}$.

3) $M = P.Q = \dfrac{\sqrt{x} + 1}{\sqrt{x} + 2} . \dfrac{\sqrt{x} + 3}{\sqrt{x} + 1}$

$= \dfrac{(\sqrt{x} + 1)(\sqrt{x} + 3)}{(\sqrt{x} + 2)(\sqrt{x} + 1)}$

$= \dfrac{\sqrt{x} + 3}{\sqrt{x} + 2} = 1 + \dfrac{1}{\sqrt{x} + 2}$

Ta có $\sqrt{x} \geq 0$ với $x \geq 0$; suy ra $\sqrt{x} + 2 \geq 2$.

Suy ra $\dfrac{1}{\sqrt{x} + 2} \leq \dfrac{1}{2}$

Do đó, $M \leq 1 + \dfrac{1}{2} = \dfrac{3}{2}$

Dấu "=" xảy ra khi $\sqrt{x} = 0$ tức là $x = 0$ (thỏa mãn điều kiện).

Vậy giá trị lớn nhất của $M$ là $\dfrac{3}{2}$ khi $x = 0$.

Hướng dẫn giải:

1) Giải phương trình $x^4 - 7x^2 + 12 = 0$.

Đặt $t = x^2$ với $t \geq 0$.

Khi đó phương trình trở thành: $ t^2 - 7t + 12 = 0 $ (1)

$\Delta_t = (-7)^2 - 4.1.12 = 1 > 0$

Vậy phương trình (1) có hai nghiệm phân biệt:

$ t_1 = \dfrac{7 + \sqrt{1}}{2.1} = 4$ (thỏa mãn);

$t_2 = \dfrac{7 - \sqrt{1}}{2.1} = 3 $ (thỏa mãn).

⚡ Với $t = 4$ thì $x^2 = 4$ suy ra  $x = \pm 2$

⚡ Với $t = 3$ thì $x^2 = 3$ suy ra $x = \pm \sqrt{3}$

Vậy tập nghiệm của phương trình là: $S = \{-\sqrt{3}; \sqrt{3}; -2; 2\}$.

2) a) $\Delta = [- (2m - 1)]^2 - 4(m - 1) = 4m^2 - 4m + 1 - 4m + 4 $

$ = 4m^2 - 8m + 5 = 4(m - 1)^2 + 1 > 0 $

Vậy phương trình (1) luôn có hai nghiệm phân biệt.

b) Phương trình (1) luôn có hai nghiệm phân biệt $x_1, \, x_2$ nên theo hệ thức Vietè, ta có:

$ x_1 + x_2 = 2m - 1$ và $x_1 x_2 = m - 1$

Theo đề bài, ta có: $ x_1^3 + x_2^3 = 2m^2 - m $

$(x_1 + x_2). (x_1^2 - x_1 x_2 + x_2^2) = 2m^2 - m $

$ (2m - 1) . [ (x_1 + x_2)^2 - 3x_1 x_2 ] = 2m^2 - m $

$(2m - 1) .[ (2m - 1)^2 - 3(m - 1) ] = 2m^2 - m $

$(2m - 1) .(4m^2 - 4m + 1 - 3m + 3) = 2m^2 - m $

$(2m - 1) . (4m^2 - 7m + 4) = 2m^2 - m $

$(2m - 1)(4m^2 - 7m + 4) - (2m^2 - m) = 0 $

$(2m - 1)(4m^2 - 7m + 4) - 2m^2 + m = 0 $

$(2m - 1)(4m^2 - 7m + 4) = 2m^2 - m $

Giải phương trình này, ta được: $ m = 1$ hoặc $ m = \dfrac{1}{2} $.

Vậy $m \in \Big\{ 1, \dfrac{1}{2} \Big\}$ thỏa mãn yêu cầu đề bài.

Hướng dẫn giải:

Gọi số ha rừng lâm trường dự định trồng trong mỗi tuần là $x$ (ha; $x > 0$).

Thời gian trồng rừng theo kế hoạch là: $ \dfrac{75}{x}$ (tuần)

Thời gian trồng rừng thực tế là: $ \dfrac{80}{x + 5}$ (tuần)

Vì thực tế hoàn thành sớm hơn dự định $7$ ngày $=1$ tuần nên ta có phương trình:

$\dfrac{75}{x} - \dfrac{80}{x + 5} = 1$

$ x^2 + 10x - 375 = 0 $

$ (x - 15)(x + 25) = 0 $

$ x = 15 $ (thỏa mãn) hoặc $x = -25$ (loại)

Vậy số ha rừng lâm trường dự định trồng trong một tuần là $15$ ha.

Hướng dẫn giải:

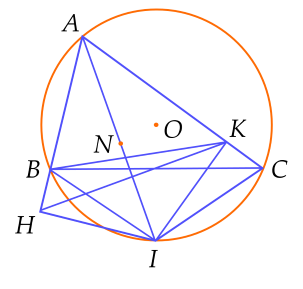
1) Gọi $N$ là trung điểm của $AI$.

Ta có $IH \perp AB$ suy ra $\widehat{IHA} = 90^\circ$

Tam giác $AHI$ vuông tại $H$ có trung tuyến $HN$ ứng với cạnh huyền nên $AN = NI = NH = \dfrac12 AI$ (1)

Ta có $IK \perp  AC$ suy ra $\widehat{AKI} = 90^\circ

Tam giác $AKI$ vuông tại $K$ có trung tuyến $KN$ ứng với cạnh huyền nên $AN = NI = NK = \dfrac12 AI$ (2)

Từ (1) và (2) suy ra  $AN = NI = NK = NH$ hay bốn điểm $A, \, H, \, I, \, K$ cùng thuộc đường tròn đường kính $AI$.

2) Ta có $I$ là điểm chính giữa cung nhỏ $BC$ suy ra $\widehat{IB} = \widehat{IC}$ hay $\widehat{IAB} = \widehat{IAC}$.

Xét $\Delta IAH$ và $\Delta IAK$ có:

$\widehat{IHA} = \widehat{IKA} = 90^\circ$ (giả thiết)

$IA$ chung

Do đó, $\Delta IAH = \Delta IAK$ (c.g.c)

Suy ra $IH = IK$ nên $\Delta IHK $ cân tại $I $.

Ta có $AHIK$ là tứ giác nội tiếp nên $\widehat{HAK} + \widehat{HIK} = 180^\circ$.

$ABIC$ là tứ giác nội tiếp nên $\widehat{BAC} + \widehat{BIC} = 180^\circ$.

Suy ra $\widehat{IHK} = \widehat{BIC} $.

Hướng dẫn giải:

Đặt $t = \sqrt[3]{x^3 - 2} x^3 - 2 = t^3$ (2)

Từ (1) trở thành: $ 5x^2 - 12x + 6 - 2t^2 + 5t = 0 $

$ 5x^2 - 12x + 6 = 2t^2 - 5t$ (3)

Lấy (2) trừ (3) ta có: $ x^3 - 5x^2 + 12x - 8 = t^3 - 2t^2 + 5t $

$ (x^3 - 6x^2 + 12x - 8) - (t^3 - 3t^2 + 3t - 1) + t^2 - 2t + 1 = 0 $

$ (x - 2)^3 - (t - 1)^3 + (t + 1)^2 = 0$ (4) $

Đặt $ a = x - 2, \, b = t - 1 $ suy ra $x = a + 2, \, t = b + 1 $

Suy ra (4) trở thành: $ a^3 + (a + 2)^2 = b^3 + (b + 2)^2 $

$ a^3 - b^3 + (a + 2)^2 - (b + 2)^2 = 0 $

$ (a - b)(a^2 + ab + b^2) + (a + 2 - b - 2)(a + 2 + b + 2) = 0 $

$ (a - b)(a^2 + ab + b^2) + (a - b)(a + b + 4) = 0 $

$ (a - b) ( a^2 + ab + b^2 + a + b + 4) = 0 $

$ (a - b) \left[ (a + b)^2 + 6 \right] = 0 $

$ a = b $

⚡ Với $a = b$ ta có: $x - 2 = t - 1$ hay $t = x - 1$

⚡ Với $t = x - 1$ ta có: $ \sqrt[3]{x^3 - 2} = x - 1 $

$ x^3 - 2 = (x - 1)^3 $

$ 3x^2 - 3x - 1 = 0 $

$ x = \dfrac{3 \pm \sqrt{21}}{6}$.

Vậy tập nghiệm của phương trình (1) là $S = \Big\{ \dfrac{3- \sqrt{21}}{6}; \dfrac{3 + \sqrt{21}}{6}\Big\}$.