Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra số 3 (100% tự luận) SVIP
1) (2 điểm) Biểu đồ cột hình dưới đây cho biết cỡ giày của các bạn nam khối 9 trong trường.
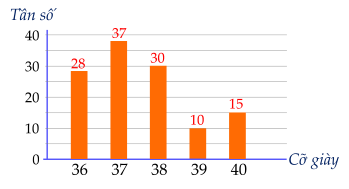
Lập bảng tần số và bảng tần số tương đối cho dữ liệu được biểu diễn trên biểu đồ (Làm tròn đến hàng phần mười).
2) (1 điểm) Chọn ngẫu nhiên một số tự nhiên có bốn chữ số đôi một khác nhau. Tính số phần tử của không gian mẫu.
Hướng dẫn giải:
1) Bảng tần số và bảng tần số tương đối cho dữ liệu cỡ giày của các bạn nam khối 9 trong trường.
|
Cỡ giày |
$36$ |
$37$ |
$38$ |
$39$ |
$40$ |
|
|
Tần số |
$28$ |
$37$ |
$30$ |
$10$ |
$15$ |
$N=120$ |
|
Tần số tương đối |
$23,3\%$ |
$30,8\%$ |
$25\%$ |
$8,4\%$ |
$12,5\%$ |
$N=100\%$ |
2) Gọi số cần tìm là $\overline{a_1a_2a_3a_4}$ trong đó $a_i \in \mathbb{N},$ $0\le a_i \le 9, \, a_1\ne 0$ là các chữ số.
Chọn $a_1$ có $9$ cách.
Chọn $a_2$ có $9$ cách.
Chọn $a_3$ có $8$ cách.
Chọn $a_4$ có $7$ cách.
Số cách chọn là $9.9.8.7=4 \, 536$ cách.
Vậy số phần tử của không gian mẫu là $4 \, 536$.
(3 điểm) Cho hai biểu thức $A=\dfrac{2}{\sqrt{x}-1}$ và $B=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{4}{x-1}$ với $x\ge 0,\, x \ne 1.$
a) Tính giá trị của biểu thức $A$ khi $x=4.$
b) Rút gọn biểu thức $P=B-A.$
c) Tìm giá trị nhỏ nhất của biểu thức $P.$
Hướng dẫn giải:
a) Tính giá trị của biểu thức $A$ khi $x=4.$
Thay $x=4$ (thỏa mãn điều kiện) vào biểu thức $A$ ta được:
$A=\dfrac{2}{\sqrt{4}-1}=2.$
b) Với $x\ge 0,\,x \ne 1$ ta có $P=B-A=\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{4}{x-1}-\dfrac{2}{\sqrt{x}-1}$
$=\dfrac{\sqrt{x}\left( \sqrt{x}-1 \right)+4-2\left( \sqrt{x}+1 \right)}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}$
$=\dfrac{x-3\sqrt{x}+2}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}$
$=\dfrac{\left( \sqrt{x}-1 \right)\left( \sqrt{x}-2 \right)}{\left( \sqrt{x}-1 \right)\left( \sqrt{x}+1 \right)}$
$=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}.$
c) Với $x\ge 0, \, x \ne 1$ ta có $P=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}=1-\dfrac{3}{\sqrt{x}+1}.$
$\sqrt{x}+1\ge 1$ với mọi $x$ thỏa mãn điều kiện nên $\dfrac{3}{\sqrt{x}+1} \le 3$ suy ra $P\ge -2.$
Dấu bằng xảy ra khi và chỉ khi $x=0$ (thỏa mãn điều kiện).
Vậy giá trị nhỏ nhất của biểu thức $P=-2$ khi $x=0.$
(2 điểm) Cho đường tròn $(O)$ đường kính $AB$. Trên tiếp tuyến tại $A$ của đường tròn $(O)$ lấy điểm $C$. Vẽ cát tuyến $CDE$ của đường tròn $( O)$ (tia $CD$ nằm giữa hai tia $CA, \, CO$ và điểm $D$ nằm giữa hai điểm $C$ và $E$). Gọi $M$ là giao điểm của $CO$ và $BD$; $H$ là hình chiếu vuông góc của $A$ trên $CO$.
a) Chứng minh tứ giác $ADMH$ là tứ giác nội tiếp.
b) Chứng minh $CD.CE=CH. CO$.
Hướng dẫn giải:
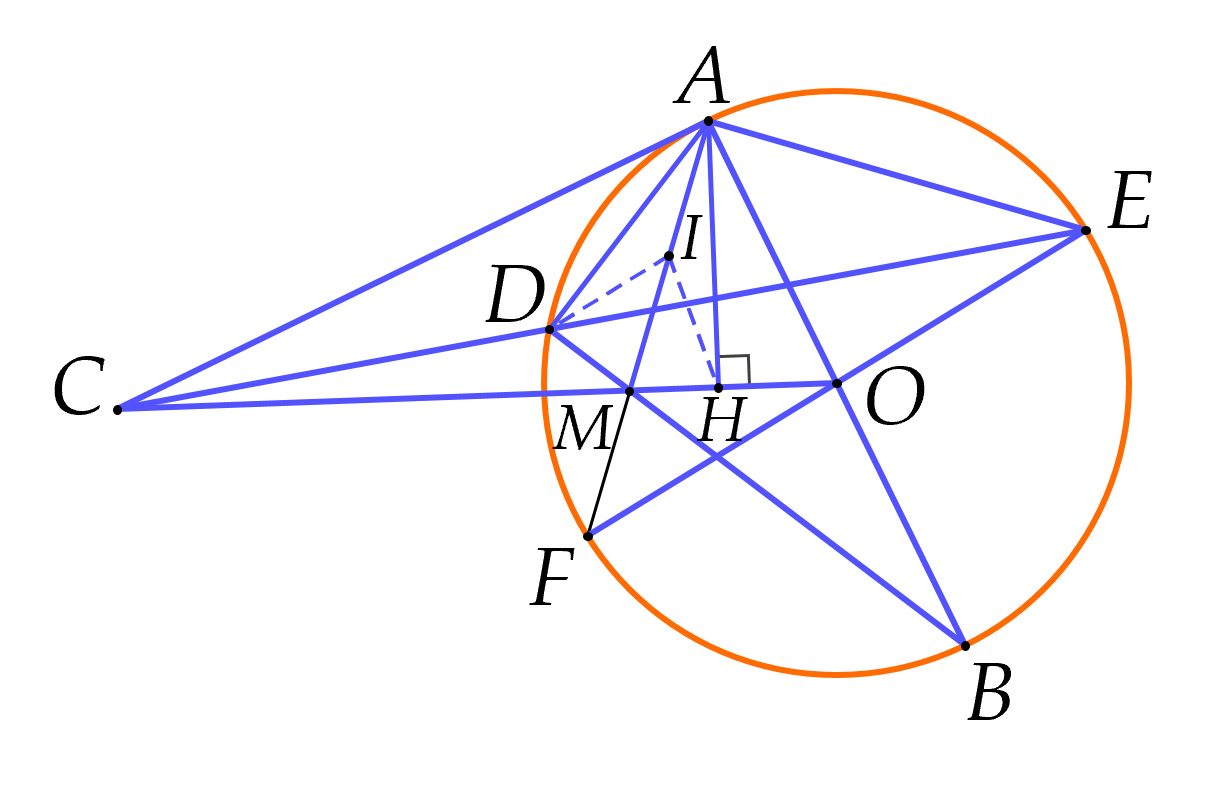
a) Gọi $I$ là trung điểm của $AM$.
Ta có $\widehat{ADB}=90^\circ $ (góc nội tiếp chắn nửa đường tròn) hay $\widehat{ADM}=90^\circ$
Suy ra $\Delta ADM$ là tam giác vuông tại $D$ có $DI$ là đường trung tuyến nên $AI=DI=MI= \dfrac{AM}{2}$ (1)
Do $H$ là hình chiếu vuông góc của điểm $A$ trên $CO$ nên $AH \bot CO$
Suy ra $\Delta AHM$ là tam giác vuông tại $H$ có $HI$ là đường trung tuyến nên: $AI=HI=MI= \dfrac{AM}{2}$ (2)
Từ (1) và (2) suy ra $AI=DI=MI=HI$,
Do đó bốn điểm $A; \, D; \, M; \, H$ cùng thuộc một đường tròn.
Vậy $ADMH$ là tứ giác nội tiếp.
b) Ta có $\widehat{CAD}+\widehat{DAO}=90^\circ $
$\widehat{CEA}+\widehat{CEB}=\widehat{AEB}=90^\circ $ (góc nội tiếp chắn nửa đường tròn).
Mà $\widehat{DAO}=\widehat{CEB}$ (cùng chắn $\overset\frown{DB}$)
Do đó $\widehat{CAD}=\widehat{CEA}$
Do đó $ \Delta CAD \backsim \Delta CEA$ (g.g)
Suy ra $\dfrac{CA}{CE}=\dfrac{CD}{CA}$ hay $CA^2=CD.CE$ (1)
Mặt khác $\Delta ACO \backsim \Delta HCA$ (g.g)
Suy ra $CA^2=CH.CO$ (2)
Từ (1) và (2) suy ra: $CD.CE=CH.CO$.
(1 điểm) Một vườn rau hình chữ nhật $MNPQ$ có diện tích $640$ m2, để tạo cảnh quan đẹp mắt người ta mở rộng thêm $4$ phần diện tích để trồng hoa, tạo thành đường tròn ngoại tiếp như hình vẽ biết tâm hình tròn trùng với tâm hình chữ nhật.
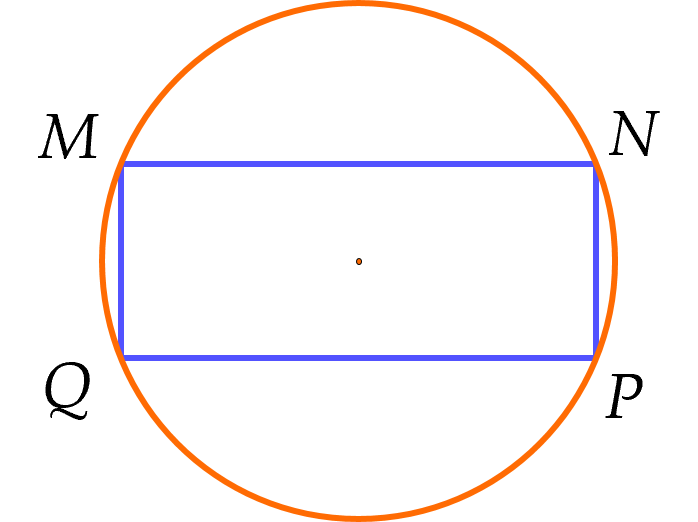
Tính diện tích nhỏ nhất của $4$ phần đất được trồng thêm hoa (kết quả làm tròn đến chữ số thập phân thứ hai).
Hướng dẫn giải:
Gọi giao điểm hai đường chéo của hình chữ nhật là $O$.
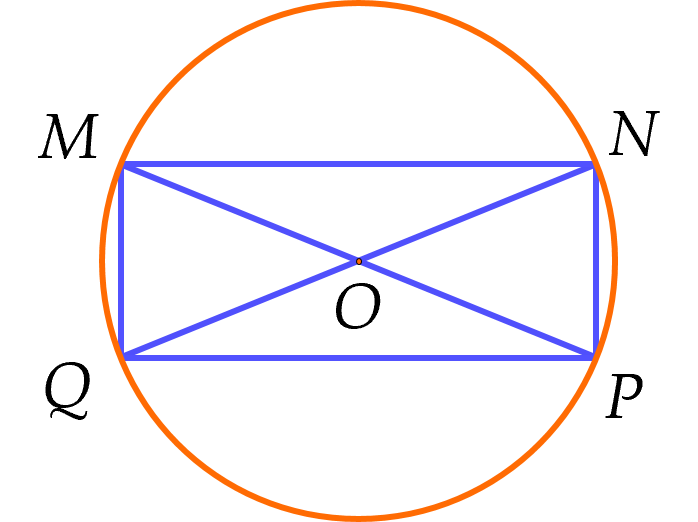
Gọi $x, \, y$ (m) lần lượt là hai kích thước của mảnh vườn $(x>0,\,y>0)$ và $R$ (m) là bán kính đường tròn ngoại tiếp mảnh vườn.
Áp dụng định lí Pythagore trong tam giác vuông $MNP$, ta có:
$x^2+y^2=MP^2$
Suy ra $R^2=OM^2=\dfrac{x^2+y^2}{4}$
Theo đề bài $xy=640$ m2
Diện tích $4$ phần đất mở rộng là: $S=S_t-S_{MNPQ}=\pi R^2-xy=\pi .\Big( \dfrac{x^2+y^2}{4} \Big)-xy \ge \pi . \dfrac{2xy}{4}-xy$ (theo bất đẳng thức Cauchy)
Do đó $S\ge 320\pi -640\approx 365,31$ m2.
Dấu "=" xảy ra khi $x=y=8\sqrt{10}$ (thoả mãn).
Vậy diện tích nhỏ nhất của $4$ phần đất được trồng thêm hoa khoảng $365,31$ m2.
(1 điểm) Trên một đường tròn cho 21 điểm phân biệt. Mỗi một điểm được tô bởi 1 trong 4 màu: xanh, đỏ, tím, vàng. Giữa mỗi cặp điểm nối với nhau bằng một đoạn thẳng được tô bởi một trong 2 màu: nâu hoặc đen. Chứng minh rằng luôn tồn tại một tam giác có ba đỉnh được tô cùng một màu (xanh, đỏ, tím hoặc vàng) và ba cạnh cũng được tô cùng một màu (nâu hoặc đen).
Hướng dẫn giải:
Vì các điểm phân biệt nằm trên một đường tròn nên ba điểm bất kì luôn tạo thành một tam giác.
Có 21 điểm được tô bằng 4 màu, do đó có ít nhất 6 điểm có cùng màu.
Giả sử có 6 điểm cùng màu đỏ là $A,B,C,D,E,F$
Nối 5 đoạn $AB,AC,AD,AE,AF$ và tô bằng hai màu nâu, đen khi đó có ít nhất 3 đoạn cùng màu, giả sử $AB,AC,AD$ được tô cùng màu đen
Xét $\Delta BCD$, xảy ra hai khả năng:
TH1: Nếu 3 cạnh $BC,BD,DC$ được tô cùng màu nâu thì tam giác $BCD$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu nâu (thỏa mãn)
TH2: Nếu ba cạnh $BC,BD,DC$ có ít nhất một cạnh màu đen, giả sử $BC$ đen, khi đó tam giác $ABC$ có ba đỉnh cùng màu đỏ, ba cạnh cùng màu đen (thỏa mãn)
Vậy luôn có một tam giác có ba đỉnh cùng màu và ba cạnh cùng màu.
