Đề số 2 (cấu trúc mới)

Câu 1 (1đ):

Tập xác định của hàm số $f\left(x \right)=\dfrac{3x-6}{4x-12}$ là

D=\mathbb{R}\backslash \left\{ 3 \right\}

.

D=\mathbb{R}

.

D=\mathbb{R}\backslash \left\{ 2 \right\}

.

D=\left(3;+\infty \right)

.

Câu 2 (1đ):

Tọa độ giao điểm của parabol $\left(P \right)$ : $y=x^2-6x+5$ với trục hoành là

\left(0;1 \right);

\left(5;0 \right)

.

\left(1;0 \right)

;

\left(5;0 \right)

.

\left(0;1 \right);

\left(0;5 \right)

.

\left(1;0 \right)

;

\left(0;5 \right)

.

Câu 3 (1đ):

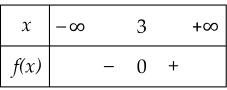
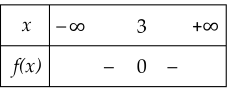
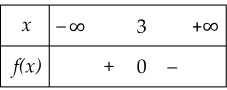
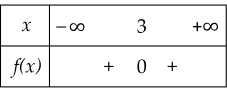
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức $f\left( x \right)=-{{x}^{2}}+6x-9$ ?

Câu 4 (1đ):

Tủ lạnh nhà bạn Đô có $20$ hộp sữa và $15$ cái bánh quy, trong đó có $12$ hộp sữa có hương dâu và $8$ hộp sữa sô cô la, $8$ cái bánh quy hương sô cô la và $7$ cái bánh quy hương dâu. Bạn Đô đang cần lựa $1$ món bánh sô cô la và $1$ hộp sữa dâu để ăn bữa chiều thì Đô có bao nhiêu cách chọn?

35

.

84

.

15

.

96

.

Câu 5 (1đ):

Trong khai triển $\left( 2x+1 \right)^5$ hệ số của số hạng chứa $x^5$ là

1 \, 000

.

10

.

100

.

32

.

Câu 6 (1đ):

Trong mặt phẳng $Oxy,$ côsin góc giữa hai đường thẳng $d: \, 5x+y-3=0$ và ${d}': \, \dfrac{x}{-1}+\dfrac{y}{5}=1$ bằng

\dfrac{6}{13}

.

0

.

\dfrac{12}{13}

.

-\dfrac{12}{13}

.

Câu 7 (1đ):

Cho đường tròn $\left(C \right): \, x^2+y^2-6x+4y-12=0$ . Đường tròn $\left(C \right)$ có tâm $I$ và bán kính $R$ lần lượt là

I\left(-6;\,4 \right), \, R=5

.

I\left(-3;\,2 \right), \, R=5

.

I\left(6;\,-4 \right), \, R=5

.

I\left(3;\,-2 \right), \, R=5

.

Câu 8 (1đ):

Trong mặt phẳng tọa độ $Oxy$ cho đường tròn $\left(C \right)$ có phương trình $x^2+y^2-4x+2y=0$ và điểm $M\left(1;1 \right)$ thuộc đường tròn $\left(C \right)$ . Phương trình tiếp tuyến của đường tròn $\left(C \right)$ tại điểm $M\left(1;1 \right)$ là đường thẳng

x+2y+1=0

.

x-2y-1=0

.

x-2y+1=0

.

x+y-1=0

.

Câu 9 (1đ):

Parabol $\left(P \right): \, y^2=8x$ có tiêu điểm

F\left(2\,;\,0 \right)

.

F\left(0\,;\,2 \right)

.

F\left(-2\,;\,0 \right)

.

F\left(0\,;\,-2 \right)

Câu 10 (1đ):

Hành động nào dưới đây là một phép thử ngẫu nhiên?

Gieo 3 con xúc xắc.

Rút một lá bài từ cỗ bài tú lơ khơ cho đến khi xuất hiện quân K thì dừng lại.

Gieo một con xúc xắc cho đến khi xuất hiện mặt 5 chấm thì dừng lại.

Gieo một đồng xu cho đến khi xuất hiện mặt sấp thì dừng lại.

Câu 11 (1đ):

Phương trình $\sqrt{x^2+2x-3}=5-x$ có nghiệm là $x=\dfrac{a}{b}$ . Khi đó $a+2b$ bằng

13

.

10

.

33

.

17

.

Câu 12 (1đ):

Một tổ học sinh có $7$ nam và $3$ nữ. Chọn ngẫu nhiên $2$ người. Xác suất sao cho $3$ học sinh được chọn có đúng một học sinh nữ là

\dfrac{21}{40}

.

\dfrac{7}{120}

.

\dfrac{7}{40}

.

\dfrac{7}{15}

.

Câu 13 (1đ):

Cho elip có phương trình chính tắc $\dfrac{x^2}{25}+\dfrac{y^2}{9}=1$ .

(Nhấp vào dòng để chọn đúng / sai)

Elip có tiêu cự bằng $8$ .
Elip có tiêu điểm $F_1\left(-4;0 \right)$ .
Điểm $A\left(5;3\right)$ thuộc đường elip.
$MF_1+MF_2=12$ , với $M$ là một điểm thuộc đường elip.

Câu 14 (1đ):

Trong hệ trục tọa độ $Oxy$ , cho điểm $I\left(1;1 \right)$ và đường thẳng $\left(d \right):3x+4y-2=0$ .

(Nhấp vào dòng để chọn đúng / sai)

Khoảng cách từ điểm $I\left(1;1 \right)$ đến đường thẳng $\left(d \right):3x+4y-2=0$ bằng $1$ .
Đường tròn tâm $I\left(1;1 \right)$ và tiếp xúc với đường thẳng $\left(d \right):3x+4y-2=0$ có phương trình chính tắc là ${{\left(x-1 \right)}^{2}}+{{\left(y-1 \right)}^{2}}=1$ .
Đường tròn tâm $I\left(1;1 \right)$ và tiếp xúc với đường thẳng $\left(d \right):3x+4y-2=0$ có phương trình tổng quát là ${{x}^{2}}+{{y}^{2}}-2x-2y+1=0$ .
Đường thẳng đi qua điểm $I\left(1;1 \right)$ và vuông góc với đường thẳng $\left(d \right):3x+4y-2=0$ có phương trình tổng quát là $3x+4y-7=0$ .

Câu 15 (1đ):

Cho tập $S=\{1;\,2;\,3;\,4;\,5\}$ .

(Nhấp vào dòng để chọn đúng / sai)

a) Lập được $60$ số có $3$ chữ số khác nhau từ tập $S$ .
b) Lập được $9$ số có $5$ chữ số khác nhau lấy từ tập $S$ , sao cho số đó chia hết cho $5$ và số đứng đầu là $1$ .
c) Lập được $100$ số có $3$ chữ số từ tập $S$ nhỏ hơn $225$ .
d) Lập được $320$ số có $4$ chữ số từ tập $S$ sao cho số các chữ số giống nhau không được đứng cạnh nhau.

Câu 16 (1đ):

Một hộp có $5$ viên bi xanh, $6$ viên bi đỏ và $7$ viên bi vàng. Xét phép thử chọn ngẫu nhiên $3$ viên bi.

(Nhấp vào dòng để chọn đúng / sai)

Không gian mẫu của phép thử là: $816$ .
Xác suất để chọn được $3$ viên bi đỏ là $\dfrac{1}{272}$ .
Xác suất để chọn được $3$ viên bi gồm $3$ màu là $\dfrac{35}{136}$ .
Xác suất chọn được nhiều nhất $2$ viên bi xanh là $\dfrac{403}{408}$ .

Câu 17 (1đ):

Trong một dịp quay xổ số, có ba loại giải thưởng: 1 000 000 đồng, 500 000 đồng, 100 000 đồng. Nơi bán có $100$ tờ vé số, trong đó có $1$ vé trúng thưởng 1 000 000 đồng, $5$ vé trúng thưởng 500 000 đồng, $10$ vé trúng thưởng 100 000 đồng. Một người mua ngẫu nhiên $3$ vé. Tính xác suất của biến cố "Người mua đó trúng thưởng ít nhất 300 000 đồng". (Làm tròn kết quả tới chữ số thập phân thứ ba)

Trả lời:

Câu 18 (1đ):

Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang học của máy ảnh được đặt tại một tiêu điểm của gương (xem hình).

loading...

Tìm khoảng cách từ quang tâm của máy ảnh đến đỉnh của gương, biết rằng phương trình cho mặt cắt của gương là ${\dfrac{x^2}{25}-\dfrac{y^2}{16}=1}$ . (Làm tròn đến chữ số thập phân thứ hai)

Trả lời:

Câu 19 (1đ):

Phương trình chính tắc của elip đi qua điểm $M(2 \sqrt{3} ; 2)$ và $M$ nhìn hai tiêu điểm của elip dưới một góc vuông có dạng $(E): \, \dfrac{x^2}{m}+\dfrac{y^2}{n}=1$ . Tính $m - n$ .

Trả lời:

Câu 20 (1đ):

Trong mặt phẳng toạ độ ${O x y}$ , vị trí của một chất điểm ${K}$ tại thời điểm $t$ (với $0 \leq t \leq 180$ ) có toạ độ là $\left(3+2 \cos t^{\circ} ; 4+2 \sin t^{\circ}\right)$ . Biết quỹ đạo chuyển động của chất điểm $K$ là đường tròn tâm $I(a ; b)$ , bán kính $R$ . Tính $a + b +R$ .

Trả lời:

Câu 21 (1đ):

Ông $A$ có $800$ triệu đồng và ông $B$ có $950$ triệu đồng gửi hai ngân hàng khác nhau với lãi suất lần lượt là $7 \%$ /năm và $5 \%$ /năm. Dùng tổng hai số hạng đầu tiên trong khai triển của nhị thức Newton, ước lượng sau một thời gian thì số tiền của hai ông thu được là bằng nhau và mỗi người khi đó nhận được là bao nhiêu tỉ đồng?

Trả lời: tỉ đồng.

Câu 22 (1đ):

Một người đang chơi cầu lông có khuynh hướng phát cầu với góc $30^{\circ}$ (so với mặt đất). Tính khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa), biết cầu rời mặt vợt ở độ cao $0,8$ m so với mặt đất và vận tốc xuất phát của cầu là $6$ m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng và làm tròn kết quả tới hàng phần trăm).

Trả lời: m

Bài học cùng chủ đề

Đề số 2 (cấu trúc mới) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 2 (cấu trúc mới) SVIP

Tải đề xuống bằng file Word

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP