Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Đề số 2 (Phần trắc nghiệm 3 điểm) SVIP
Hệ thống phát hiện có sự thay đổi câu hỏi trong nội dung đề thi.
Hãy nhấn vào để xóa bài làm và cập nhật câu hỏi mới nhất.
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Đây là bản xem thử, hãy nhấn Bắt đầu làm bài để bắt đầu luyện tập với OLM
Câu 1 (1đ):
Bậc và hệ số của đơn thức −1,5ax2 (với a là hằng số, x là biến) lần lượt là
1,5a và bậc 3.
1,5 và bậc 2.
−1,5a và bậc 2.
−1,5 và bậc 2.
Câu 2 (1đ):
Đa thức nào sau đây không phải là đa thức bậc 4?
4xy2z.
x4−35.
x4−21xy3z.
xy2+xyzt.
Câu 3 (1đ):
Đẳng thức nào sau đây là hằng đẳng thức?
a−2=2−a.
(−x)2−x=x+x2.
x(x−1)=x−x2.
(a−b)2=(b−a)2.
Câu 4 (1đ):
Thu gọn đa thức (2x+y)(4x2−2xy+y2) ta được
x3−8y3.
8x3−y3.
2x3−y3.
8x3+y3.
Câu 5 (1đ):
Biểu thức (x+51)2 bằng
x2−21x+−41.
x2+21x+81.
x2−52x+41.
x2+52x+251.
Câu 6 (1đ):
Cho hình vẽ sau. Chọn câu đúng trong các câu sau

A
Điểm M nằm trong tứ giác ABCD và điểm N nằm ngoài tứ giác ABCD.
B
Điểm M nằm ngoài tứ giác ABCD và điểm N nằm trong tứ giác ABCD.
C
Hai đỉnh kề nhau của tứ giác ABCD là A, C.
D
Hai cạnh kề nhau của tứ giác ABCD là AB, CD.
Câu 7 (1đ):
Điền vào dấu ... để hoàn thành khẳng định: "Tứ giác có ... là hình chữ nhật."
bốn cạnh bằng nhau.
hai góc vuông.
bốn góc vuông.
các cạnh đối song song.
Câu 8 (1đ):
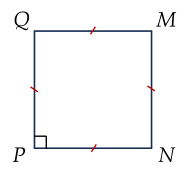
Tứ giác trên là hình vuông theo dấu hiệu nhận biết nào sau đây?
Hình thoi có một góc vuông.
Hình chữ nhật có hai đường chéo vuông góc với nhau.
Hình thoi có hai đường chéo bằng nhau.
Hình chữ nhật có hai cạnh kề bằng nhau.
Câu 9 (1đ):
Đơn thức nào dưới đây không phải đơn thức thu gọn?
61x2yxz4.
2.
x2y5.
−5x4y3z2.
Câu 10 (1đ):
Biểu thức nào dưới đây là đa thức thu gọn?
3x+2x3−4x4−x2+1+x2.
2x3y+3xy3−5+x−231.
2x2y−x2y+25x2y.
2+xy+x2y2−x2.
Câu 11 (1đ):
| x2y+z; | −x; | 0; | 2,5xyxz; | 0,35y24x |
Trong các biểu thức trên, có bao nhiêu biểu thức là đơn thức thu gọn?
2.
3.
4.
1.
Câu 12 (1đ):
Giá trị của biểu thức (x2−5)(x+3)+(x+4)(x−x2) tại x=0 là
−10.
−17.
−13.
−15.
OLMc◯2022
