Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề số 6 (TN- ĐS- TLN) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Cho hình vẽ dưới đây:
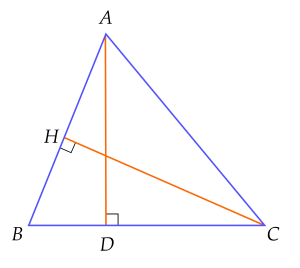
Hệ thức đúng là
Cho tam giác ABC vuông tại A có AB=5 cm, AC=12 cm và BC=13 cm.
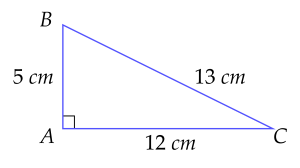
Khi đó tỉ số lượng giác sinB có giá trị bằng
Gieo xúc xắc 100 lần và thu được bảng tần số tương đối như sau:
Số chấm | Tần số tương đối |
1 | 15% |
2 | 23% |
3 | 10% |
4 | 22% |
5 | 17% |
6 | 13% |
Số lần xuất hiện mặt 6 chấm là
Chọn ngẫu nhiên một số nguyên dương nhỏ hơn 100. Gọi A là biến cố "Số được chọn chia hết cho 4". Số các kết quả thuận lợi cho A là
Cho biết a<b, đẳng thức nào dưới đây đúng?
Rút gọn biểu thức A=6−25 ta được kết quả là
Cho biết x≤3 là nghiệm của bất phương trình nào sau đây?
Điểm nào dưới đây thuộc đồ thị hàm số y=−3x2?
Biết rằng phương trình x2−5x+2=0 có hai nghiệm x1;x2. Khi đó x12+x22 bằng
Cho hình cầu có đường kính d=6 cm. Diện tích mặt cầu là
Cho hình vẽ sau:
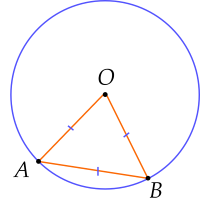
Số đo của cung nhỏ AB là
Biểu đồ hình quạt tròn dưới đây biểu diễn kết quả (tính theo phần trăm) chọn môn thể thao ưa thích nhất trong bốn môn: Cầu lông, Bóng bàn, Bóng chuyền, Bóng đá của 200 học sinh lớp 9 ở một trường trung học cơ sở (mỗi học sinh chỉ được chọn một môn thể thao khi được hỏi ý kiến).
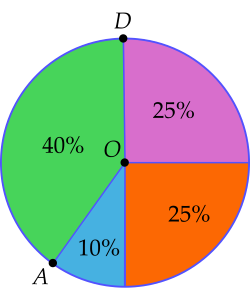
Số đo của AOD là
Cho phương trình 21x−2y=−1 (1)
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Cặp số (2;1) là nghiệm của phương trình (1). |
|
| b) Cặp số (1;41) là nghiệm của phương trình (1). |
|
| c) Áp dụng quy tắc chuyển vế ta thu được phương trình 2y=21x+1. |
|
| d) Công thức nghiệm của phương trình (1) là ⎩⎨⎧x∈Zy=41x+21. |
|
Cho hình vẽ dưới đây:
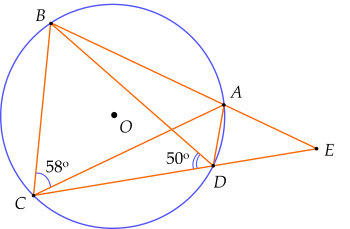
Biết BDC=50∘; BCA=58∘.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) BAC=50∘. |
|
| b) CDA=100∘. |
|
| c) CBE=72∘. |
|
| d) số đo CDA⌢=72∘. |
|
Một nhóm khách vào cửa hàng bán trà sữa. Nhóm khách đó đã mua 6 ly trà sữa gồm trà sữa trân châu và trà sữa phô mai. Giá mỗi ly trà sữa trân châu, trà sữa phô mai lần lượt là 33000 đồng và 28000 đồng. Tổng số tiền nhóm khách thanh toán cho cửa hàng là 188000 đồng. Gọi số cốc trà sữa trân châu, trà sữa phô mai lần lượt là x,y (cốc)
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Điều kiện của x,y là x,y>0. |
|
| b) Ta có x+y=6. |
|
| c) Theo bài ra, ta có hệ phương trình {x+y=628x+33y=188. |
|
| d) Nhóm khách hàng đã mua 4 cốc trà sữa trân châu và 2 cốc trà sữa phô mai. |
|
Cuối học kì II, cô giáo chủ nhiệm thống kê điểm môn Toán của lớp 9A như sau:
7 | 8 | 8 | 9 | 7 | 6 | 6 | 5 |
8 | 7 | 7 | 8 | 9 | 5 | 5 | 6 |
7 | 9 | 10 | 9 | 10 | 6 | 8 | 7 |
5 | 5 | 6 | 7 | 8 | 8 | 9 | 5 |
6 | 6 | 7 | 8 | 8 | 9 | 10 | 8 |
| a) Bảng số liệu trên có 6 giá trị khác nhau. |
|
| b) Lớp 9A có 50 học sinh. |
|
c) Từ bảng trên ta có bảng tần số 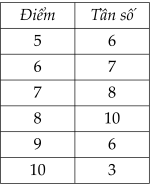
|
|
| d) Tần số tương đối của số học sinh đạt điểm 10 là 10%. |
|
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (O-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một cái giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-léch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy một tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
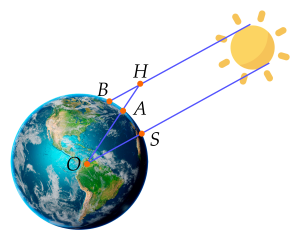
Từ hai quan sát trên, ông có thể tính xấp xỉ "chu vi" của Trái Đất bằng bao nhiêu km? (trên hình, điểm O là tâm Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).
Trả lời:
Khi điều tra về môn học được yêu thích nhất trong bốn môn: Toán, Ngữ văn, Tiếng Anh, Khoa học tự nhiên của 40 bạn trong lớp, Hiếu thống kê kết quả biểu diễn bởi biểu đồ sau:
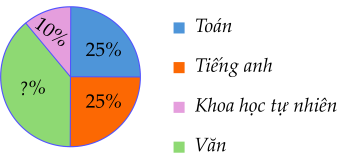
Có bao nhiêu học sinh yêu thích môn Văn?
Trả lời:
Cho hai biểu thức A=38−50−(2−1)2 và B=(x−1x−x−x1).x+11 (với x>0;x=1). Có bao nhiêu giá trị của x để A=2B?
Trả lời:
Xếp ngẫu nhiên 3 bạn Thỏ, Sóc, Rùa lần lượt đi qua một chiếc cầu. Xác suất để bạn Thỏ đi trước là bao nhiêu? (kết quả làm tròn đến chữ số thập phân thứ hai).
Trả lời:
Cho phương trình x2+ax+b=0 có hai nghiệm là 2 và −1. Khi đó giá trị biểu thức A=a2+b2 bằng bao nhiêu?
Trả lời:
Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A.
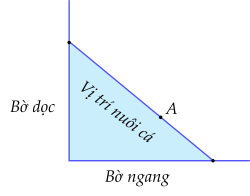
Biết rằng, khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m. Diện tích nhỏ nhất có thể giăng là bao nhiêu m2?
Trả lời:
