Bộ đề thi Toán 12 cuối kì 2 sách mới Cánh diều

Câu 1 (1đ):

Đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{x - 1}{x^{2} + x}$

y = 0;y = 1

.

y = 0;y = - 1

.

x = 0;x = 1

.

x = 0;x = - 1

.

Câu 2 (1đ):

Hàm số nào trong các hàm số sau đây không là nguyên hàm của hàm số $y = x^{2\,022}$ ?

\dfrac{x^{2\,023}}{2\,023} - 2\,025

.

y = \dfrac{x^{2\,021}}{2\,022}

.

\dfrac{x^{2\,023}}{2\,023}

.

\dfrac{x^{2\,023}}{2\,023} + 2\,024

.

Câu 3 (1đ):

Biết $\displaystyle \int_{1}^{3}{f(x)\mathrm{d}x} = 3$ . Giá trị của $\displaystyle \int_{1}^{3}{4f(x)\mathrm{d}x}$ bằng

5

.

12

.

9

.

\dfrac{3}{2}

.

Câu 4 (1đ):

Trong không gian

Oxyz

, phương trình chính tắc của đường thẳng

AB

với

A(1;1;2)

và

B( - 4;3; - 2)

là

\dfrac{x + 4}{1} = \dfrac{y - 3}{- 2} = \dfrac{z + 2}{- 2}

.

\dfrac{x + 4}{- 5} = \dfrac{y - 3}{2} = \dfrac{z + 2}{- 4}

.

\dfrac{x - 1}{1} = \dfrac{y - 1}{- 2} = \dfrac{z - 2}{- 2}

.

\dfrac{x + 1}{- 5} = \dfrac{y + 1}{2} = \dfrac{z + 2}{- 4}

.

Câu 5 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho mặt cầu $(S):(x + 1)^{2} + (y - 2)^{2} + (z - 1)^{2} = 9$ . Bán kính $R$ của $(S)$ bằng

R=\sqrt3

.

R = 9

.

R=6

.

R = 3

.

Câu 6 (1đ):

Nghiệm của phương trình

\log_{5}(2x - 1) = \log_{5}3

là

x = 62

.

x = 2

.

x = 1

.

x = 12

.

Câu 7 (1đ):

Cho cấp số cộng

\left( u_{n} \right)

với

u_{1} = 3,

u_{2} = 5

. Công sai của cấp số cộng đã cho bằng

\dfrac{3}{5}

.

\dfrac{5}{3}

.

- 2

.

2

.

Câu 8 (1đ):

Đạo hàm của hàm số $y = x^{4} - 2.\sin x$

y' = 4x^{3} - 2.\sin x

.

y' = 3x^{4} - 2.\cos x

.

y' = 4x^{3} - 2.\cos x

.

y' = 4x^{3} + 2.\cos x

.

Câu 9 (1đ):

Gọi $Q_{1},Q_{2},Q_{3}$ là tứ phân vị thứ nhất, tứ phân vị thứ hai và thứ ba của mẫu số liệu ghép nhóm. Khoảng tứ phân vị của mẫu số liệu ghép nhóm là

\Delta Q = Q_{1} - Q_{3}

.

\Delta Q = Q_{2} - Q_{1}

.

\Delta Q = Q_{3} - Q_{1}

.

\Delta Q = Q_{1} - Q_{2}

.

Câu 10 (1đ):

Trong không gian $Oxyz$ , cho ba điểm $A(3;\, 0;0\,)\,,\, B(0;\, - 1;\, 0\,)\,\,,\, C(0;\, 0;\, 2\,)$ . Mặt phẳng $(\alpha)$ đi qua $A\,,\, B,\, C$ có phương trình là

\dfrac{x}{3} + \dfrac{y}{- 1} + \dfrac{z}{2} = 1\,

.

\dfrac{x}{3} + \dfrac{y}{- 1} + \dfrac{z}{2} = 0

.

\dfrac{x}{3} + \dfrac{y}{- 1} + \dfrac{z}{2} = - 1\,

.

\dfrac{x}{- 3} + \dfrac{y}{1} + \dfrac{z}{- 2} = 1\,

.

Câu 11 (1đ):

Trong không gian $Oxyz$ , côsin của góc giữa hai đường thẳng có phương trình lần lượt là ${{d}_{1}}:\dfrac{x}{2}=\dfrac{y}{1}=\dfrac{z}{-1},$ ${{d}_{2}}:\dfrac{x-1}{3}=\dfrac{y-1}{3}=\dfrac{z-1}{9}$ bằng

0.

-\dfrac{1}{2}.

\dfrac{1}{2}.

1.

Câu 12 (1đ):

Cho tứ diện $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $B$ , biết $AD = 2a,AB = BC = a$ , cạnh bên $SA$ vuông góc với đáy và $SA = \dfrac{a\sqrt{6}}{2}$ . Gọi $E$ là trung điểm của $AD$ . Số đo của góc phẳng nhị diện $\lbrack S;BE;A\rbrack$ là

60^\circ

.

120^\circ

.

30^\circ

.

45^\circ

.

Câu 13 (1đ):

Trong không gian $Oxyz$ , cho hai điểm $A(0;2; - 1)$ và $B(3;2; - 4)$ và mặt phẳng $(P):2x + 2y + z - 6 = 0$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Một vectơ chỉ phương của đường thẳng $AB$ là $\overrightarrow{a} = (1;0; - 1)$ .
b) Đường thẳng $AB$ và mặt phẳng $(P)$ cắt nhau tại $B$ .
c) Góc (làm tròn đến hàng đơn vị của độ) giữa đường thẳng $AB$ và mặt phẳng $(P)$ là $14^{\circ}$ .
d) Đường thẳng $\Delta$ đi qua $A$ và vuông góc với mặt phẳng $(P)$ có phương trình chính tắc là $\dfrac{x}{2} = \dfrac{y - 2}{2} = \dfrac{z + 1}{1}$ .

Câu 14 (1đ):

Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:

Thời gian (phút)	Số học sinh lớp 11A	Số học sinh lớp 11B
$[0,5 ; 10,5)$	$2$	$3$
$[10,5 ; 20,5)$	$10$	$8$
$[20,5 ; 30,5)$	$6$	$10$
$[30,5 ; 40,5)$	$4$	$2$
$[40,5 ; 50,5)$	$3$	$4$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số trung bình của mẫu số liệu lớp 11A là: $23,9$ (làm tròn đến hàng phần mười).
b) Độ lệch chuẩn của mẫu số liệu lớp 11A là: $11,77$ (làm tròn đến hàng phần trăm).
c) Độ lệch chuẩn của mẫu số liệu lớp 11B là: $11,55$ (làm tròn đến hàng phần trăm).
d) Nếu so sánh theo độ lệch chuẩn thì thời gian để học sinh hoàn thành một câu hỏi thi của lớp 11A ít phân tán hơn lớp 11B

Câu 15 (1đ):

Một chiếc hộp có $80$ viên bi, trong đó có $50$ viên bi màu đỏ và $30$ viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có $60\%$ số viên bi màu đỏ đánh số và $50\%$ số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số viên bi màu đỏ có đánh số là $30$ .
b) Số viên bi màu vàng không đánh số là $15$ .
c) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là $\dfrac{3}{5}$ .
d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không đánh số là $\dfrac{7}{16}$ .

Câu 16 (1đ):

Cho hình lăng trụ tam giác $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh bằng $a$ , tam giác $AB'C'$ cân tại $A$ , mặt phẳng $(AB'C')$ vuông góc với mặt phẳng $(A'B'C')$ và $AA' = a\sqrt{3}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Mặt bên $BCC'B'$ là hình chữ nhật.
b) Hình chiếu vuông góc của $A$ trên mặt phẳng $(A'B'C')$ là trọng tâm của tam giác $A'B'C'$ .
c) Thể tích khối lăng trụ $ABC.A'B'C'$ bằng $\dfrac{3a^{3}\sqrt{3}}{8}$ .
d) Khoảng cách giữa đường thẳng $AA'$ và mặt phẳng $BC'$ bằng $\dfrac{a\sqrt{3}}{2}$ .

Câu 17 (1đ):

Người ta truyền nhiệt cho một bình nuôi cấy vi sinh vật từ $1^{\circ}C$ . Tốc độ tăng nhiệt độ của bình tại thời điểm $t$ phút $(0 \leq t \leq 5)$ được cho bởi hàm số $f(t) = 3t^{2}$ ( $^{\circ}C/$ phút $)$ . Biết rằng nhiệt độ của bình đó tại thời điểm $t$ là một nguyên hàm của hàm số $f(t)$ . Tìm nhiệt độ của bình tại thời điểm 3 phút kể từ khi truyền nhiệt.

Trả lời:

Câu 18 (1đ):

Một ô tô đang chạy với tốc độ $25$ (m/s) thì gặp chướng ngại vật, người lái xe đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc $v(t)=-5t+20$ (m/s), trong đó $t$ là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét (Làm tròn kết quả đến hàng phần mười)?

Trả lời:

Câu 19 (1đ):

Cho hàm số $y = \mathrm{e}^{x}( x^{2} - 3)$ , gọi $M = \dfrac{a}{\mathrm{e}^{b}}, \, \left( a \in\mathbb{ N}; \, b\in\mathbb{ N} \right)$ là giá trị lớn nhất của hàm số trên đoạn $\lbrack - 5; - 2\rbrack$ . Tính giá trị của biểu thức $P = a + b$ ?

Trả lời:

Câu 20 (1đ):

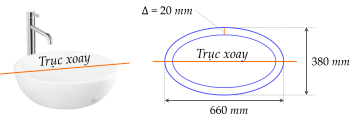
Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc, xây dựng, thiết bị nội thất,... Mặt trong (lọt lòng) và ngoài (phủ bì) của một bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi quay quanh một trục của HAI elip có chung các trục đối xứng (hình minh họa). Thông số kĩ thuật mặt trên của bồn rửa: dài $\times$ rộng là $660 \times 380$ mm (phủ bì) và elip (lọt lòng) có trục lớn, trục nhỏ ít hơn elip phủ bì một khoảng $40$ mm. Tính thể tích chứa nước của bồn rửa (đơn vị: lít) (làm tròn kết quả đến hàng phần mười).

bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi quay quanh một trục của 2 elip

Trả lời:

Câu 21 (1đ):

Một kiến trúc sư muốn xây dựng một tòa nhà biểu tượng độc đáo cho thành phố. Trên bản thiết kế tòa nhà có hình dạng là một khối lăng trụ tam giác đều $ABC.A^{'}B^{'}C^{'}$ , có cạnh bên bằng cạnh đáy và dài $30$ mét. Kiến trúc sư muốn xây dựng một cây cầu $MN$ bắc xuyên tòa nhà (điểm đầu thuộc cạnh $A^{'}C$ , điểm cuối thuộc cạnh $BC^{'}$ ) và cây cầu này sẽ được dát vàng với đơn giá $5$ tỷ đồng trên mỗi mét dài. Vì vậy để đáp ứng bài toán kinh tế, kiến trúc sư phải chọn vị trí cây cầu sao cho $MN$ ngắn nhất (như hình vẽ).

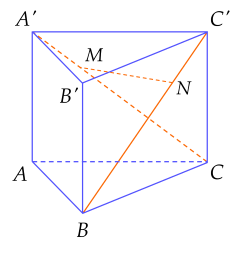
Khi đó giá xây cây cầu này hết bao nhiêu tỷ đồng? (Kết quả làm tròn đến hàng đơn vị).

Trả lời:

Câu 22 (1đ):

Cho hình chóp $S.ABC$ , có $SA = 2a$ và $SA\bot(ABC)$ . Tam giác $ABC$ vuông cân tại $B$ có $AB = a$ . Gọi $O$ là trung điểm $AC$ và $I$ là trung điểm $BC$ . Tính khoảng cách giữa các cặp đường thẳng $OI$ và $SC$ khi $a = 5$ (Kết quả làm tròn đến hàng phần trăm)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra số 4 SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra số 4 SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP